
【題目】如圖,已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為4的正方形,
是邊長為4的正方形,![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 是線段
是線段![]() 上一點,求三棱錐
上一點,求三棱錐![]() 的體積.
的體積.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題分析:(1)要證明面面垂直,只需在一個平面內找到另一平面的一條垂線.由已知平面![]() 平面
平面![]() ,且
,且![]() ,可證
,可證![]() 平面
平面![]() ,再根據
,再根據![]() 是中位線,可證
是中位線,可證![]() ,從而
,從而![]() 平面
平面![]() ,進而再證平面
,進而再證平面![]() 平面
平面![]() ,該題實質是先找到面
,該題實質是先找到面![]() 的一條垂線
的一條垂線![]() ,再將
,再將![]() 平移到面
平移到面![]() 內;
內;
(2)點![]() 是線段
是線段![]() 的動點,考慮到
的動點,考慮到![]() 和
和![]() 到面
到面![]() 的距離相等,故
的距離相等,故![]() ,再結合第(1)問結果,取
,再結合第(1)問結果,取![]() 的中點
的中點![]() 連接
連接![]() ,據面面垂直的性質,點
,據面面垂直的性質,點![]() 到
到![]() 的距離就是三棱錐
的距離就是三棱錐![]() 的高,再求
的高,再求![]() ,進而求體積.
,進而求體積.
試題解析:(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,又
,又![]() 中,
中,![]() 分別是
分別是![]() 的中點,
的中點,![]() ,可得
,可得![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,因此
,因此![]() 上的點
上的點![]() 到平面
到平面![]() 的距離等于點
的距離等于點![]() 到平面
到平面![]() 的距離,∴
的距離,∴![]() ,取
,取![]() 的中點
的中點![]() 連接
連接![]() ,則
,則![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,∴
,∴![]() ,于是
,于是![]() ,
,
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 是正三角形,∴點
是正三角形,∴點![]() 到平面
到平面![]() 的距離等于正
的距離等于正![]() 的高,即為
的高,即為![]() ,因此,三棱錐M﹣EFG的體積
,因此,三棱錐M﹣EFG的體積![]() =
=![]() =
=![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+ ![]() +b(x≠0),其中a,b∈R.若對任意的a∈[
+b(x≠0),其中a,b∈R.若對任意的a∈[ ![]() ,2],不等式f(x)≤10在x∈[
,2],不等式f(x)≤10在x∈[ ![]() ,1]上恒成立,則b的取值范圍為明 .
,1]上恒成立,則b的取值范圍為明 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解人們對于國家新頒布的“生育二胎放開”政策的熱度,現在某市進行調查,隨機調查了50人,他們年齡的頻數分布及支持“生育二胎”人數如表:
年齡 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上統計數據填下面2乘2列聯表,并問是否有的99%把握認為以45歲為分界點對“生育二胎放開”政策的支持度有差異:
(2)若對年齡在[5,15),[35,45)的被調查人中各隨機選取兩人進行調查,記選中的4人不支持“生育二胎”人數為ξ,求隨機變量ξ的分布列及數學期望;
年齡不低于45歲的人數 | 年齡低于45歲的人數 | 合計 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合計 |
參考數據:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知命題![]() :實數
:實數![]() 滿足
滿足![]() ,命題
,命題![]() :實數
:實數![]() 滿足方程
滿足方程![]() 表示的焦點在
表示的焦點在![]() 軸上的橢圓,且
軸上的橢圓,且![]() 是
是![]() 的充分不必要條件,求實數
的充分不必要條件,求實數![]() 的取值范圍;
的取值范圍;
(2)設命題![]() :關于
:關于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ;
;![]() :函數
:函數![]() 的定義域為
的定義域為![]() .若
.若![]() 是真命題,
是真命題,![]() 是假命題,求實數
是假命題,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,BC= ![]() ,AB=AC=AA1=1,D是棱CC1上的一點,P是AD的延長線與A1C1的延長線的交點,且PB1∥平面BDA1 .
,AB=AC=AA1=1,D是棱CC1上的一點,P是AD的延長線與A1C1的延長線的交點,且PB1∥平面BDA1 . 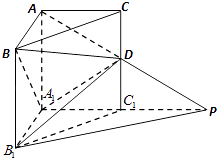
(1)求證:CD=C1D;
(2)求二面角A1﹣B1D﹣P的平面角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,右頂點、上頂點分別為點
,右頂點、上頂點分別為點![]() ,
,
已知橢圓![]() 的焦距為
的焦距為![]() ,且
,且![]() .
.

(1)求橢圓![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,當
兩點,當![]() 面積取得最大時,求直線
面積取得最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=﹣x2+alnx(a∈R).
(1)當a=2時,求函數f(x)在點(1,f(1))處的切線方程;
(2)若函數g(x)=f(x)﹣2x+2x2 , 討論函數g(x)的單調性;
(3)若(2)中函數g(x)有兩個極值點x1 , x2(x1<x2),且不等式g(x1)≥mx2恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com