
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),解方程
時(shí),解方程![]() .
.
(2)當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根據(jù)對(duì)數(shù)運(yùn)算法則化簡(jiǎn)原方程得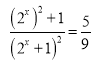 ,再令
,再令![]() ,則原方程化為
,則原方程化為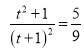 整理得
整理得![]() 求解可得原方程的解,注意對(duì)數(shù)函數(shù)的定義域;
求解可得原方程的解,注意對(duì)數(shù)函數(shù)的定義域;
(2)由![]() 化簡(jiǎn)不等式為
化簡(jiǎn)不等式為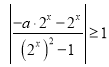 ,令
,令![]() ,當(dāng)
,當(dāng)![]() 時(shí),得
時(shí),得![]() ,所以當(dāng)
,所以當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,等價(jià)于
恒成立,等價(jià)于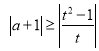 在
在![]() 時(shí)恒成立,再令
時(shí)恒成立,再令![]() ,證明函數(shù)
,證明函數(shù)![]() 在
在![]() 上單調(diào)遞增,并得出在
上單調(diào)遞增,并得出在![]() 上的最值,建立關(guān)于
上的最值,建立關(guān)于![]() 的不等式
的不等式![]() ,可得實(shí)數(shù)
,可得實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
(1)當(dāng)![]() 時(shí),
時(shí),![]() ,
,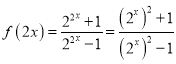 ,
,
所以方程![]() 化為
化為![]() 且
且![]() ,即
,即![]() 且
且 ,
,![]() ,
,
所以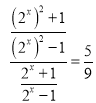 ,即
,即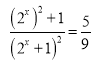 ,
,
令![]() ,則原方程化為
,則原方程化為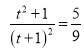 整理得
整理得![]() ,
,
解得![]() 或
或![]() ,即
,即![]() 或
或![]() ,解得
,解得![]() 或
或![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),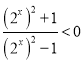 ,
,![]() ,故舍去,
,故舍去,
故原方程的解為:![]() ;
;
(2)由![]() 得
得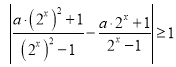 ,即
,即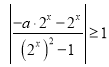 ,
,
令![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,所以
,所以![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,等價(jià)于當(dāng)
恒成立,等價(jià)于當(dāng)![]() 時(shí),
時(shí),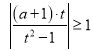 恒成立,即
恒成立,即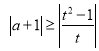 在
在![]() 時(shí)恒成立,
時(shí)恒成立,
令![]() ,設(shè)
,設(shè)![]() ,
,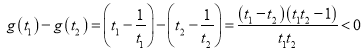 ,
,
所以![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
解得![]() 或
或![]() ;
;
所以實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() 或
或![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知圓O:![]() 和點(diǎn)
和點(diǎn)![]() ,由圓O外一點(diǎn)P向圓O引切線
,由圓O外一點(diǎn)P向圓O引切線![]() ,Q為切點(diǎn),且有
,Q為切點(diǎn),且有![]() .
.
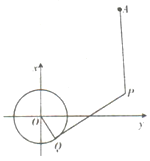
(1)求點(diǎn)P的軌跡方程,并說(shuō)明點(diǎn)P的軌跡是什么樣的幾何圖形?
(2)求![]() 的最小值;
的最小值;
(3)以P為圓心作圓,使它與圓O有公共點(diǎn),試在其中求出半徑最小的圓的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點(diǎn).

(Ⅰ)證明: BC1//平面A1CD;
(Ⅱ)設(shè)AA1= AC=CB=2,AB=2![]() ,求三棱錐C一A1DE的體積.
,求三棱錐C一A1DE的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在底面半徑為6的圓柱內(nèi),有兩個(gè)半徑也為6的球面,兩球的球心距為13,若作一個(gè)平面與兩個(gè)球都相切,且與圓柱面相交成一橢圓,則橢圓的長(zhǎng)軸長(zhǎng)為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知點(diǎn)![]() ,圓
,圓![]() .
.
(1)若直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() 且到圓心
且到圓心![]() 的距離為
的距離為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設(shè)過(guò)點(diǎn)![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn)(
兩點(diǎn)(![]() 的斜率為負(fù)),當(dāng)
的斜率為負(fù)),當(dāng)![]() 時(shí),求以線段
時(shí),求以線段![]() 為直徑的圓的方程.
為直徑的圓的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖為某大河的一段支流,岸線![]() 近似滿足
近似滿足![]() ∥
∥![]() 寬度為7
寬度為7![]() 圓
圓![]() 為河中的一個(gè)半徑為2
為河中的一個(gè)半徑為2![]() 的小島,小鎮(zhèn)
的小島,小鎮(zhèn)![]() 位于岸線
位于岸線![]() 上,且滿足岸線
上,且滿足岸線![]() 現(xiàn)計(jì)劃建造一條自小鎮(zhèn)
現(xiàn)計(jì)劃建造一條自小鎮(zhèn)![]() 經(jīng)小島
經(jīng)小島![]() 至對(duì)岸
至對(duì)岸![]() 的通道
的通道![]() (圖中粗線部分折線段,
(圖中粗線部分折線段,![]() 在
在![]() 右側(cè)),為保護(hù)小島,
右側(cè)),為保護(hù)小島,![]() 段設(shè)計(jì)成與圓
段設(shè)計(jì)成與圓![]() 相切,設(shè)
相切,設(shè)![]()
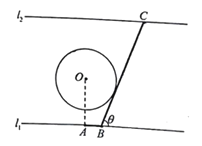
(1)試將通道![]() 的長(zhǎng)
的長(zhǎng)![]() 表示成
表示成![]() 的函數(shù),并指出其定義域.
的函數(shù),并指出其定義域.
(2)求通道![]() 的最短長(zhǎng).
的最短長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在抗擊新型冠狀病毒肺炎期間,為響應(yīng)政府號(hào)召,郴州市某單位組織了志愿者30人,其中男志愿者18人,用分層抽樣的方法從該單位志愿者中抽取5人去參加某社區(qū)的防疫幫扶活動(dòng).
(1)求從該單位男、女志愿者中各抽取的人數(shù);
(2)從抽取的5名志愿者中任選2名談此活動(dòng)的感受,求選出的2名志愿者中恰有1名男志愿者的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知袋子中放有大小和形狀相同的小球若干,其中標(biāo)號(hào)為0的小球1個(gè),標(biāo)號(hào)為1的小球1個(gè),標(biāo)號(hào)為2的小球![]() 個(gè).若從袋子中隨機(jī)抽取1個(gè)小球,取到標(biāo)號(hào)為2的小球的概率是
個(gè).若從袋子中隨機(jī)抽取1個(gè)小球,取到標(biāo)號(hào)為2的小球的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)從袋子中不放回地隨機(jī)抽取2個(gè)小球,記第一次取出的小球標(biāo)號(hào)為![]() ,第二次取出的小球標(biāo)號(hào)為
,第二次取出的小球標(biāo)號(hào)為![]() .
.
①記“![]() ”為事件
”為事件![]() ,求事件
,求事件![]() 的概率;
的概率;
②在區(qū)間![]() 內(nèi)任取2個(gè)實(shí)數(shù)
內(nèi)任取2個(gè)實(shí)數(shù)![]() ,
,![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 時(shí),
時(shí),![]() 的值域:
的值域:
(3)設(shè)![]() ,若
,若![]() 對(duì)任意的
對(duì)任意的![]() ,總有
,總有![]() 恒成立,求實(shí)數(shù)a的取值范圍.
恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com