Question

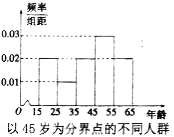
【題目】為了了解人們對“延遲退休年齡政策”的態度，某部門從網年齡在15~65歲的人群中隨機調查100人，調查數據的頻率分布直方圖和支持“延遲退休”的人數與年齡的統計結果如下：

（I）由頻率分布直方圖估計年齡的眾數和平均數；

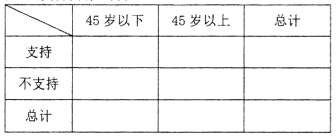
（II）由以上統計數據填2×2列聯表，并判斷是否有95%的把握認為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異；

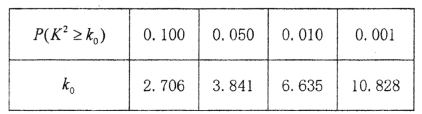
參考數據：

（III）若以45歲為分界點，從不支持“延遲退休”的人中按分層抽樣的方法抽取8人參加某項活動.現從這8人中隨機抽2人.求抽到的2人中1人是45歲以下，另一人是45歲以上的概率.

Answer 1

【答案】（Ⅰ）眾數為50，平均數為42，（Ⅱ）有95%的把握 (Ⅲ)

【解析】

（Ⅰ）根據頻率分布直方圖知，最高矩形的中點代表的是眾數，矩形中點乘以矩形面積求和可得平均數；

（Ⅱ）由統計數據填寫列聯表，計算觀測值，對照臨界值得出結論；
(Ⅲ) 設45歲以下的6人為a1，a2， a3，a4， a5，a6，45歲以上的2人為b1，b2，將所有的基本事件列舉出來，數出滿足條件的基本事件，利用古典概型計算公式求解即可．

解：(I) 估計眾數為50.

估計平均數為＝20×0.2＋30×0.1＋40×0.2＋50×0.3＋60×0.2＝42.

(II)列聯表如下：

	45歲以下	45歲以上	總計
支持	35	45	80
不支持	15	5	20
總計	50	50	100

因為K2＝＝＝6.25＞3.841，

所以有95%的把握認為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異．

(III)從不支持“延遲退休”的人中抽取8人，則45歲以下的應抽6人，45歲以上的應抽2人．

設45歲以下的6人為a1，a2， a3，a4， a5，a6，45歲以上的2人為b1，b2，則從這8人中隨機抽2人包含以下基本事件(a1，a2)，(a1，a3)，(a1，a4)，(a1，a5)，(a1，a6)，(a1，b1)，(a1，b2)，(a2，a3)，(a2，a4)，(a2，a5)， (a2，a6)，(a2，b1)，(a2，b2)，(a3，a4)，(a3，a5)，(a3，a6)，(a3，b1)，(a3，b2)，(a4，a5)，(a4，a6)，(a4，b1)，(a4，b2)，(a5，a6)，(a5，b1)，(a5，b2)，(a6，b1)，(a6，b2)，( (b1，b2)共28個基本事件．記抽到的2人中1人是45歲以下，另一人是45歲以上為事件M，則事件M包含如下基本事件(a1，b1)，(a1，b2)，(a2，b1)，(a2，b2)，(a3，b1)，(a3，b2)，(a4，b1)，(a4，b2)，(a5，b1)，(a5，b2)，(a6，b1)，(a6，b2)，共12個基本事件．故.

即抽到的2人中1人是45歲以下，另一人是45歲以上的概率為.