
【題目】直角坐標系xoy中,曲線![]() :
:![]() (
(![]() :y=kx (x
:y=kx (x![]() ),以坐標原點為極點,x軸正半軸為極軸建立坐標系,曲線
),以坐標原點為極點,x軸正半軸為極軸建立坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為:![]() .
.
(1)求![]() 的直角坐標方程。
的直角坐標方程。
(2)![]() 曲線
曲線![]() 交于點B,求A、B兩點的距離。
交于點B,求A、B兩點的距離。
【答案】(1) C1:(X-2)![]() +(y-1)
+(y-1)![]() =5,
=5,![]() ;(2)
;(2)![]() .
.
【解析】
(1)根據(jù)平方和消參求![]() 的直角坐標方程,由極坐標與直角坐標互化的公式即可求得
的直角坐標方程,由極坐標與直角坐標互化的公式即可求得![]() 的直角坐標方程;
的直角坐標方程;
(2)由于曲線![]() 過原點和另一點,可以求出其斜率,再將曲線
過原點和另一點,可以求出其斜率,再將曲線![]() 化為極坐標形式,
化為極坐標形式,
令曲線![]() 分別與另兩條曲線的極坐標方程聯(lián)立,求出
分別與另兩條曲線的極坐標方程聯(lián)立,求出![]() ,
,
由![]() ,即可求出結果.
,即可求出結果.
(1)C1:(X-2)![]() +(y-1)
+(y-1)![]() =5,
=5,![]() :
:![]() 即
即![]() .
.
(2)C2的極坐標方程θ=α(ρ≥0,θ![]()
 )又C2過點(2,1),所以tanα=
)又C2過點(2,1),所以tanα=![]() ,cosα=
,cosα=![]() ,sinα=
,sinα=![]() ,由曲線C1:(X-2)
,由曲線C1:(X-2)![]() +(y-1)
+(y-1)![]() =5 ,所以
=5 ,所以![]() -4ρcosθ-2ρsinθ=0.
-4ρcosθ-2ρsinθ=0.
與θ=α聯(lián)立得![]() -4ρcosα-2ρsinα=0 ρ
-4ρcosα-2ρsinα=0 ρ![]() ,同理聯(lián)立C2于C3得
,同理聯(lián)立C2于C3得
3![]() cos
cos![]() α+4ρ
α+4ρ![]() sin
sin![]() α=12,得ρ
α=12,得ρ![]() =
=![]() 所以
所以![]() =ρ
=ρ![]() -ρ
-ρ![]() =2
=2![]() -
-![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知正六棱錐![]() 的底面邊長為
的底面邊長為![]() ,高為
,高為![]() .現(xiàn)從該棱錐的
.現(xiàn)從該棱錐的![]() 個頂點中隨機選取
個頂點中隨機選取![]() 個點構成三角形,設隨機變量
個點構成三角形,設隨機變量![]() 表示所得三角形的面積.
表示所得三角形的面積.
(1)求概率![]() 的值;
的值;
(2)求![]() 的分布列,并求其數(shù)學期望
的分布列,并求其數(shù)學期望![]() .
.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
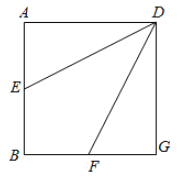
【題目】如圖,棱長為![]() 的正方形
的正方形![]() 中,點
中,點![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 上的點,且
上的點,且![]() ,將
,將![]() ,
,![]() 沿
沿![]() ,
,![]() 折起,使得
折起,使得![]() ,
,![]() 兩點重合于
兩點重合于![]() 點上,設
點上,設![]() 與
與![]() 交于
交于![]() 點,過點
點,過點![]() 作
作![]() 于
于![]() 點.
點.
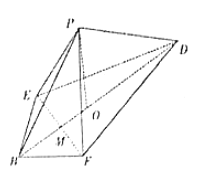
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C:![]() 的左、右焦點分別為F1,F(xiàn)2,離心率為
的左、右焦點分別為F1,F(xiàn)2,離心率為![]() ,P為橢圓C上的動點,且滿足
,P為橢圓C上的動點,且滿足![]() ,
,![]() ,
,![]() 面積的最大值為4.
面積的最大值為4.
(1)求動點Q的軌跡E的方程和橢圓C的方程.
(2)若點P不在x軸上,過點F2作OP的平行線交曲線C于M、N兩個不同的點,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在一個特定時段內(nèi),以點E為中心的7海里以內(nèi)海域被設為警戒水域.點E正北55海里處有一個雷達觀測站A.某時刻測得一艘勻速直線行駛的船只位于點A北偏東45°且與點A相距![]() 海里的位置B,經(jīng)過40分鐘又測得該船已行駛到點A北偏東
海里的位置B,經(jīng)過40分鐘又測得該船已行駛到點A北偏東![]()
 且與點A相距
且與點A相距![]() 海里的位置C.
海里的位置C.
(1)求該船的行駛速度(單位:海里/時);
(2)若該船不改變航行方向繼續(xù)行駛判斷它是否會進入警戒水域,并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】若一個四位數(shù)的各位數(shù)字相加和為![]() ,則稱該數(shù)為“完美四位數(shù)”,如數(shù)字“
,則稱該數(shù)為“完美四位數(shù)”,如數(shù)字“![]() ”.試問用數(shù)字
”.試問用數(shù)字![]() 組成的無重復數(shù)字且大于
組成的無重復數(shù)字且大于![]() 的“完美四位數(shù)”有( )個
的“完美四位數(shù)”有( )個
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列命題正確的是( )
A. 冪函數(shù)的圖象都經(jīng)過![]() 、
、![]() 兩點
兩點
B. 當![]() 時,函數(shù)
時,函數(shù)![]() 的圖象是一條直線
的圖象是一條直線
C. 如果兩個冪函數(shù)的圖象有三個公共點,那么這兩個函數(shù)一定相同
D. 如果冪函數(shù)為偶函數(shù),則圖象一定經(jīng)過點![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓![]() 經(jīng)過兩點
經(jīng)過兩點![]() ,且圓心在直線
,且圓心在直線![]() 上,直線
上,直線![]() 的方程為
的方程為![]() 。
。
(1)求圓![]() 的方程;
的方程;
(2)證明:直線![]() 與圓
與圓![]() 恒相交;
恒相交;
(3)求直線![]() 被圓
被圓![]() 截得的弦長的取值范圍。
截得的弦長的取值范圍。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】同時拋擲兩枚骰子,并記下二者向上的點數(shù),求:
![]() 二者點數(shù)相同的概率;
二者點數(shù)相同的概率;
![]() 兩數(shù)之積為奇數(shù)的概率;
兩數(shù)之積為奇數(shù)的概率;
![]() 二者的數(shù)字之和不超過5的概率.
二者的數(shù)字之和不超過5的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com