
【題目】已知集合A={x|x2-6x+8<0},B={x|(x-a)(x-3a)<0}.
(1)若x∈A是x∈B的充分條件,求a的取值范圍;
(2)若A∩B=,求a的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ∪[4,+∞)
∪[4,+∞)
【解析】試題分析:
首先求得集合A={x|2<x<4},B={x|(x-a)(x-3a)<0}.
(1)由題意分類討論a>0和a<0兩種情況可得a的取值范圍為![]() .
.
(2)由題意分類討論集合B是否為空集可得a的取值范圍是![]() ∪[4,+∞).
∪[4,+∞).
試題解析:
A={x|x2-6x+8<0}={x|2<x<4},B={x|(x-a)(x-3a)<0}.
(1)當(dāng)a=0時(shí),B=,不合題意.
當(dāng)a>0時(shí),B={x|a<x<3a},要滿足題意,
則![]() 解得
解得![]() ≤a≤2.
≤a≤2.
當(dāng)a<0時(shí),B={x|3a<x<a},要滿足題意,
則![]() 無(wú)解.綜上,a的取值范圍為
無(wú)解.綜上,a的取值范圍為![]() .
.
(2)要滿足A∩B=,
當(dāng)a>0時(shí),B={x|a<x<3a},
則a≥4或3a≤2,即0<a≤![]() 或a≥4.
或a≥4.
當(dāng)a<0時(shí),B={x|3a<x<a},則a≤2或a≥![]() ,即a<0.
,即a<0.
當(dāng)a=0時(shí),B=,A∩B=.
綜上,a的取值范圍為![]() ∪[4,+∞).
∪[4,+∞).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“累計(jì)凈化量(CCM)”是空氣凈化器質(zhì)量的一個(gè)重要衡量指標(biāo),它是指空氣凈化器從開始使用到凈化效率為![]() 時(shí)對(duì)顆粒物的累計(jì)凈化量(單位:克).根據(jù)國(guó)家標(biāo)準(zhǔn),對(duì)空氣凈化器的累計(jì)凈化量(CCM)有如下等級(jí)劃分:
時(shí)對(duì)顆粒物的累計(jì)凈化量(單位:克).根據(jù)國(guó)家標(biāo)準(zhǔn),對(duì)空氣凈化器的累計(jì)凈化量(CCM)有如下等級(jí)劃分:
累計(jì)凈化量(克) |
|
|
| 12以上 |
等級(jí) |
|
|
|
|
已知某批空氣凈化器共![]() 臺(tái),其累計(jì)凈化量都分布在區(qū)間
臺(tái),其累計(jì)凈化量都分布在區(qū)間![]() 內(nèi),為了解其質(zhì)量,隨機(jī)抽取了
內(nèi),為了解其質(zhì)量,隨機(jī)抽取了![]() 臺(tái)凈化器作為樣本進(jìn)行估計(jì),按照
臺(tái)凈化器作為樣本進(jìn)行估計(jì),按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均勻分組,其中累計(jì)凈化量在
均勻分組,其中累計(jì)凈化量在![]() 的所有數(shù)據(jù)有:
的所有數(shù)據(jù)有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,并繪制了如下頻率分布直方圖.
,并繪制了如下頻率分布直方圖.
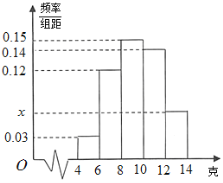
(1)求![]() 的值及頻率分布直方圖中
的值及頻率分布直方圖中![]() 的值;
的值;
(2)以樣本估計(jì)總體,試估計(jì)這批空氣凈化器(共2000臺(tái))中等級(jí)為![]() 的空氣凈化器有多少臺(tái)?
的空氣凈化器有多少臺(tái)?
(3)從累計(jì)凈化量在![]() 的樣本中隨機(jī)抽取2臺(tái),求恰好有1臺(tái)等級(jí)為
的樣本中隨機(jī)抽取2臺(tái),求恰好有1臺(tái)等級(jí)為![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù) ![]()
(1)當(dāng)a=2時(shí),求f(x)在x∈[0,1]的最大值;
(2)當(dāng)0<a<1,f(x)在x∈[0,1]上的最大值和最小值之和為a,求a的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知多面體![]() 中,四邊形
中,四邊形![]() 為平行四邊形,
為平行四邊形, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
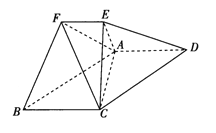
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,直線
,直線![]() 與平面
與平面![]() 夾角的正弦值為
夾角的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】給出下列四個(gè)命題:
(1)命題“若 ![]() ,則tanα=1”的逆否命題為假命題;
,則tanα=1”的逆否命題為假命題;
(2)命題p:x∈R,sinx≤1.則¬p:x0∈R,使sinx0>1;
(3)“ ![]() ”是“函數(shù)y=sin(2x+)為偶函數(shù)”的充要條件;
”是“函數(shù)y=sin(2x+)為偶函數(shù)”的充要條件;
(4)命題p:“x0∈R,使 ![]() ”;命題q:“若sinα>sinβ,則α>β”,那么(¬p)∧q為真命題.
”;命題q:“若sinα>sinβ,則α>β”,那么(¬p)∧q為真命題.
其中正確的個(gè)數(shù)是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校高三(1)班在一次單元測(cè)試中,每位同學(xué)的考試分?jǐn)?shù)都在區(qū)間[100,128]內(nèi),將該班所有同學(xué)的考試分?jǐn)?shù)分為七組:[100,104),[104,108),[108,112),[112,116),[116,120),[120,124),[124,128],繪制出頻率分布直方圖如圖所示,已知分?jǐn)?shù)低于112分的有18人,則分?jǐn)?shù)不低于120分的人數(shù)為( ) 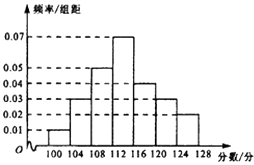
A.10
B.12
C.20
D.40
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)等差數(shù)列{an}的前n項(xiàng)和為Sn , 且S4=4S2 , a2n=2an+1.
(Ⅰ)求數(shù)列{an}的通項(xiàng)公式
(Ⅱ)設(shè)數(shù)列{bn}的前n項(xiàng)和為Tn , 且 ![]() (λ為常數(shù)).令cn=b2n , (n∈N*),求數(shù)列{cn}的前n項(xiàng)和Rn .
(λ為常數(shù)).令cn=b2n , (n∈N*),求數(shù)列{cn}的前n項(xiàng)和Rn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若二次函數(shù)![]() 的圖象和直線
的圖象和直線![]() 無(wú)交點(diǎn),現(xiàn)有下列結(jié)論:
無(wú)交點(diǎn),現(xiàn)有下列結(jié)論:
①方程![]() 一定沒有實(shí)數(shù)根;②若
一定沒有實(shí)數(shù)根;②若![]() ,則不等式
,則不等式![]() 對(duì)一切實(shí)數(shù)
對(duì)一切實(shí)數(shù)![]() 都成立;
都成立;
③若![]() ,則必存在實(shí)數(shù)
,則必存在實(shí)數(shù)![]() ,使
,使![]() ;④若
;④若![]() ,則不等式
,則不等式![]() 對(duì)一切實(shí)數(shù)都成立;⑤函數(shù)
對(duì)一切實(shí)數(shù)都成立;⑤函數(shù)![]() 的圖象與直線
的圖象與直線![]() 也一定沒有交點(diǎn),其中正確的結(jié)論是__________.(寫出所有正確結(jié)論的編號(hào))
也一定沒有交點(diǎn),其中正確的結(jié)論是__________.(寫出所有正確結(jié)論的編號(hào))
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義在![]() 上的偶函數(shù)
上的偶函數(shù)![]() ,其導(dǎo)函數(shù)為
,其導(dǎo)函數(shù)為![]() ,若對(duì)任意的實(shí)數(shù)
,若對(duì)任意的實(shí)數(shù)![]() ,都有
,都有![]() 恒成立,則使
恒成立,則使![]() 成立的實(shí)數(shù)
成立的實(shí)數(shù)![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B. (﹣∞,﹣1)∪(1,+∞)
B. (﹣∞,﹣1)∪(1,+∞)
C. (﹣1,1) D. (﹣1,0)∪(0,1)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com