
【題目】高二某班![]() 名同學期末考完試后,商量購買一些學習參考書準備在高三時使用,大家約定:每個人通過擲一枚質地均勻的骰子決定自己去哪購買,擲出點數大于或等于
名同學期末考完試后,商量購買一些學習參考書準備在高三時使用,大家約定:每個人通過擲一枚質地均勻的骰子決定自己去哪購買,擲出點數大于或等于![]() 的人去圖書批發市場購買,擲出點數小于
的人去圖書批發市場購買,擲出點數小于![]() 的人去網上購買,且參加者必須從圖書批發市場和網上選擇一家購買.
的人去網上購買,且參加者必須從圖書批發市場和網上選擇一家購買.
(1)求這![]() 人中至多有
人中至多有![]() 人去圖書批發市場購買的概率;
人去圖書批發市場購買的概率;
(2)用![]() 、
、![]() 分別表示這
分別表示這![]() 人中去圖書批發市場和網上購買的人數,記
人中去圖書批發市場和網上購買的人數,記![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
科目:高中數學 來源: 題型:
【題目】方程![]() 的曲線即為函數
的曲線即為函數![]() 的圖像,對于函數
的圖像,對于函數![]() ,有如下結論:①
,有如下結論:①![]() 在
在![]() 上單調遞減;②函數
上單調遞減;②函數![]() 不存在零點;③
不存在零點;③ ![]() 的最大值為
的最大值為![]() ;④若函數
;④若函數![]() 和
和![]() 的圖像關于原點對稱,則
的圖像關于原點對稱,則![]() 由方程
由方程![]() 確定;其中所有正確的命題序號是( )
確定;其中所有正確的命題序號是( )
A.③④B.②③C.①④D.①②
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 件產品中,有
件產品中,有![]() 件正品,
件正品,![]() 件次品,從這
件次品,從這![]() 件產品中任意抽取
件產品中任意抽取![]() 件.
件.
(1)共有多少種不同的抽法?
(2)抽出的![]() 件中恰有
件中恰有![]() 件次品的抽法有多少種?
件次品的抽法有多少種?
(3)抽出的![]() 件中至少有
件中至少有![]() 件次品的抽法有多少種?
件次品的抽法有多少種?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學高中畢業班的三名同學甲、乙、丙參加某大學的自主招生考核,在本次考核中只有合格和優秀兩個等次.若考核為合格,則給予![]() 分的降分資格;若考核為優秀,則給予
分的降分資格;若考核為優秀,則給予![]() 分的降分資格.假設甲、乙、丙考核為優秀的概率分別為
分的降分資格.假設甲、乙、丙考核為優秀的概率分別為![]() 、
、![]() 、
、![]() ,他們考核所得的等次相互獨立.
,他們考核所得的等次相互獨立.
(1)求在這次考核中,甲、乙、丙三名同學中至少有一名考核為優秀的概率;
(2)記在這次考核中,甲、乙、丙三名同學所得降分之和為隨機變量![]() ,請寫出
,請寫出![]() 所有可能的取值,并求
所有可能的取值,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某機構為了了解不同年齡的人對一款智能家電的評價,隨機選取了50名購買該家電的消費者,讓他們根據實際使用體驗進行評分.
(Ⅰ)設消費者的年齡為![]() ,對該款智能家電的評分為
,對該款智能家電的評分為![]() .若根據統計數據,用最小二乘法得到
.若根據統計數據,用最小二乘法得到![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() ,且年齡
,且年齡![]() 的方差為
的方差為![]() ,評分
,評分![]() 的方差為
的方差為![]() .求
.求![]() 與
與![]() 的相關系數
的相關系數![]() ,并據此判斷對該款智能家電的評分與年齡的相關性強弱.
,并據此判斷對該款智能家電的評分與年齡的相關性強弱.
(Ⅱ)按照一定的標準,將50名消費者的年齡劃分為“青年”和“中老年”,評分劃分為“好評”和“差評”,整理得到如下數據,請判斷是否有![]() 的把握認為對該智能家電的評價與年齡有關.
的把握認為對該智能家電的評價與年齡有關.
好評 | 差評 | |
青年 | 8 | 16 |
中老年 | 20 | 6 |
附:線性回歸直線![]() 的斜率
的斜率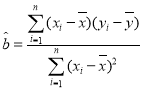 ;相關系數
;相關系數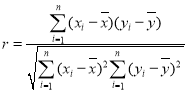 ,獨立性檢驗中的
,獨立性檢驗中的![]() ,其中
,其中![]() .
.
臨界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在下列命題中,
①從分別標有1,2,……,9的9張卡片中不放回地隨機抽取2次,每次抽取1張,則抽到的2張卡片上的數奇偶性不同的概率是![]() ;
;
②![]() 的展開式中的常數項為2;
的展開式中的常數項為2;
③設隨機變量![]() ,若
,若![]() ,則
,則![]() .
.
其中所有正確命題的序號是( )
A.②B.①③
C.②③D.①②③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 滿足
滿足![]() (
(![]() ,且
,且![]() ),且
),且![]() ,設
,設![]() ,
,![]() ,數列
,數列![]() 滿足
滿足![]() .
.
(1)求證:數列![]() 是等比數列并求出數列
是等比數列并求出數列![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前n項和
的前n項和![]() ;
;
(3)對于任意![]() ,
,![]() ,
,![]() 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com