Question

【題目】為了調查某生產線上質量監督員甲是否在現場對產品質量好壞有無影響，現統計數據如下：質量監督員甲在現場時，1 000件產品中合格品有990件，次品有10件，甲不在現場時，500件產品中有合格品490件，次品有10件．

（1）補充下面列聯表，并初步判斷甲在不在現場與產品質量是否有關：

	合格品數/件	次品數/件	總數/件
甲在現場	990
甲不在現場		10
總數/件

（2）用獨立性檢驗的方法判斷能否在犯錯誤的概率不超過0.15的前提下認為“甲在不在現場與產品質量有關”？

P(K2≥k)	0.15	0.10	0.05	0.025	0.010	0.005	0.001
K	2.072	2.706	3.841	5.024	6.635	7.879	10.828

Answer 1

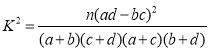
【答案】（1）列聯表如圖

	合格品數/件	次品數/件	總數/件
甲在現場	990	10	1000
甲不在現場	490	10	500
總數/件	1480	20	1500

在某種程度上可以認為甲在不在現場與產品質量有關。

（2）能在犯錯誤的概率不超過0.15的前提下認為“甲在不在現場與產品質量有關”。

【解析】

（1）先由數據得出列聯表，通過計算的值得出答案。

（2）由表中數據可得的觀測值，進而得出答案。

（1）根據題中所給數據得出列聯表如圖

	合格品數/件	次品數/件	總數/件
甲在現場	990	10	1000
甲不在現場	490	10	500
總數/件	1480	20	1500

由列聯表看出

因為相差較大，所以在某種程度上可以認為甲在不在現場與產品質量有關。

（2）由表中數據可得的觀測值

所以能在犯錯誤的概率不超過0.15的前提下認為“甲在不在現場與產品質量有關”。