
【題目】如圖,已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,以橢圓C的左頂點T為圓心作圓T:(x+2)2+y2=r2(r>0),設圓T與橢圓C交于點M與點N.
,以橢圓C的左頂點T為圓心作圓T:(x+2)2+y2=r2(r>0),設圓T與橢圓C交于點M與點N. 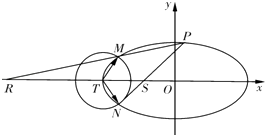
(1)求橢圓C的方程;
(2)求 ![]() 的最小值,并求此時圓T的方程;
的最小值,并求此時圓T的方程;
(3)設點P是橢圓C上異于M,N的任意一點,且直線MP,NP分別與x軸交于點R,S,O為坐標原點,求證:|OR||OS|為定值.
【答案】
(1)解:依題意,得a=2, ![]() ,
,
∴c= ![]() ,b=
,b= ![]() =1,
=1,
故橢圓C的方程為 ![]() .
.
(2)解:方法一:點M與點N關于x軸對稱,
設M(x1,y1),N(x1,﹣y1),不妨設y1>0.
由于點M在橢圓C上,所以 ![]() . (*)
. (*)
由已知T(﹣2,0),則 ![]() ,
, ![]() ,
,
∴ ![]()
=(x1+2)2﹣ ![]()
= ![]()
= ![]() .
.
由于﹣2<x1<2,
故當 ![]() 時,
時, ![]() 取得最小值為
取得最小值為 ![]() .
.
由(*)式, ![]() ,故
,故 ![]() ,
,
又點M在圓T上,代入圓的方程得到 ![]() .
.
故圓T的方程為: ![]() .
.
方法二:點M與點N關于x軸對稱,
故設M(2cosθ,sinθ),N(2cosθ,﹣sinθ),
不妨設sinθ>0,由已知T(﹣2,0),
則 ![]()
=(2cosθ+2)2﹣sin2θ
=5cos2θ+8cosθ+3
= ![]() .
.
故當 ![]() 時,
時, ![]() 取得最小值為
取得最小值為 ![]() ,
,
此時 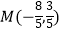 ,
,
又點M在圓T上,代入圓的方程得到 ![]() .
.
故圓T的方程為: ![]()
(3)解:方法一:設P(x0,y0),
則直線MP的方程為: ![]() ,
,
令y=0,得 ![]() ,
,
同理: ![]() ,
,
故 ![]() (**)
(**)
又點M與點P在橢圓上,
故 ![]() ,
, ![]() ,
,
代入(**)式,
得: ![]() .
.
所以|OR||OS|=|xR||xS|=|xRxS|=4為定值.
方法二:設M(2cosθ,sinθ),N(2cosθ,﹣sinθ),
不妨設sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.
則直線MP的方程為: ![]() ,
,
令y=0,得 ![]() ,
,
同理: ![]() ,
,
故 ![]() .
.
所以|OR||OS|=|xR||xS|=|xRxS|=4為定值
【解析】(1)依題意,得a=2, ![]() ,由此能求出橢圓C的方程.(2)法一:點M與點N關于x軸對稱,設M(x1 , y1),N(x1 , ﹣y1),設y1>0.由于點M在橢圓C上,故
,由此能求出橢圓C的方程.(2)法一:點M與點N關于x軸對稱,設M(x1 , y1),N(x1 , ﹣y1),設y1>0.由于點M在橢圓C上,故 ![]() .由T(﹣2,0),知
.由T(﹣2,0),知 ![]() =
= ![]() ,由此能求出圓T的方程. 法二:點M與點N關于x軸對稱,故設M(2cosθ,sinθ),N(2cosθ,﹣sinθ),設sinθ>0,由T(﹣2,0),得
,由此能求出圓T的方程. 法二:點M與點N關于x軸對稱,故設M(2cosθ,sinθ),N(2cosθ,﹣sinθ),設sinθ>0,由T(﹣2,0),得 ![]() =
= ![]() ,由此能求出圓T的方程.(3)法一:設P(x0 , y0),則直線MP的方程為:
,由此能求出圓T的方程.(3)法一:設P(x0 , y0),則直線MP的方程為: ![]() ,令y=0,得
,令y=0,得 ![]() ,同理:
,同理: ![]() ,故
,故 ![]() ,由此能夠證明|OR||OS|=|xR||xS|=|xRxS|=4為定值.
,由此能夠證明|OR||OS|=|xR||xS|=|xRxS|=4為定值.
法二:設M(2cosθ,sinθ),N(2cosθ,﹣sinθ),設sinθ>0,P(2cosα,sinα),其中sinα≠±sinθ.則直線MP的方程為: ![]() ,由此能夠證明|OR||OS|=|xR||xS|=|xRxS|=4為定值.
,由此能夠證明|OR||OS|=|xR||xS|=|xRxS|=4為定值.


科目:高中數學 來源: 題型:
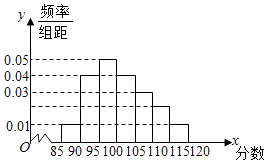
【題目】某校高二奧賽班N名學生的物理測評成績(滿分120分)分布直方圖如圖,已知分數在100~110的學生數有21人. (Ⅰ)求總人數N和分數在110~115分的人數n;
(Ⅱ)現準備從分數在110~115分的n名學生(女生占 ![]() )中任選2人,求其中恰好含有一名女生的概率;
)中任選2人,求其中恰好含有一名女生的概率;
(Ⅲ)為了分析某個學生的學習狀態,對其下一階段的學習提供指導性建議,對他前7次考試的數學成績x(滿分150分),物理成績y進行分析,下面是該生7次考試的成績.
數學 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
已知該生的物理成績y與數學成績x是線性相關的,若該生的數學成績達到130分,請你估計他的物理成績大約是多少?
附:對于一組數據(u1 , v1),(u2 , v2),,(un , vn),其回歸線v=α+βu的斜率和截距的最小二乘估計分別為 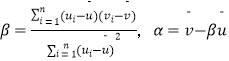 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(sin(2x+
=(sin(2x+ ![]() ),sinx),
),sinx), ![]() =(1,sinx),f(x)=
=(1,sinx),f(x)= ![]() .
.
(Ⅰ)求函數f(x)的單調遞減區間;
(Ⅱ)在△ABC中,a,b,c分別是角A,B,C的對邊,a=2 ![]() ,
, ![]() ,若
,若 ![]() sin(A+C)=2cosC,求b的大小.
sin(A+C)=2cosC,求b的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A、B、C的對邊分別為a、b、c,且 ![]() ,B=C. (Ⅰ)求cosB的值;
,B=C. (Ⅰ)求cosB的值;
(Ⅱ)設函數f(x)=sin(2x+B),求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B兩點分別在兩條互相垂直的直線y=2x和x+ay=0上,且線段AB的中點為P(0, ![]() ),則直線AB的方程為( )
),則直線AB的方程為( )
A.y=- ![]() x+5
x+5
B.y= ![]() x-5
x-5
C.y= ![]() x+5
x+5
D.y=- ![]() x-5
x-5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方體ABCD﹣A1B1C1D1中,如圖E、F分別是BB1 , CD的中點, 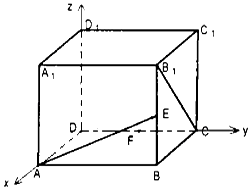
(1)求證:D1F⊥AE;
(2)求直線EF與CB1所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數f(x)=5sin3x+5 ![]() cos3x,下列說法正確的是( )
cos3x,下列說法正確的是( )
A.函數f(x)關于x= ![]() π對稱
π對稱
B.函數f(x)向左平移 ![]() 個單位后是奇函數
個單位后是奇函數
C.函數f(x)關于點( ![]() ,0)中心對稱
,0)中心對稱
D.函數f(x)在區間[0, ![]() ]上單調遞增
]上單調遞增
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com