
(本小題滿分14分)若函數(shù) ,
,
(1)當(dāng) 時,求函數(shù)
時,求函數(shù) 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(2)函數(shù) 是否存在極值.
是否存在極值.
解:(1)由題意,函數(shù) 的定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/6b/f/emhnc2.gif" style="vertical-align:middle;" /> ………………2分
的定義域?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/6b/f/emhnc2.gif" style="vertical-align:middle;" /> ………………2分
當(dāng) 時,
時, ,
, ……3分
……3分
令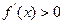 ,即
,即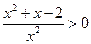 ,得
,得 或
或 ………………5分
………………5分
又因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/ae/7/1burs2.gif" style="vertical-align:middle;" />,所以,函數(shù) 的單調(diào)增區(qū)間為
的單調(diào)增區(qū)間為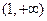 ………………6分
………………6分
(2) ……………7分
……………7分
解法一:令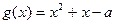 ,因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/3c/7/iz3sc1.gif" style="vertical-align:middle;" />對稱軸
,因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/3c/7/iz3sc1.gif" style="vertical-align:middle;" />對稱軸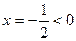 ,所以只需考慮
,所以只需考慮 的正負(fù),
的正負(fù),
當(dāng) 即
即 時,在(0,+∞)上
時,在(0,+∞)上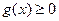 ,
,
即 在(0,+∞)單調(diào)遞增,
在(0,+∞)單調(diào)遞增, 無極值 ………………10分
無極值 ………………10分
當(dāng) 即
即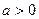 時,
時, 在(0,+∞)有解,所以函數(shù)
在(0,+∞)有解,所以函數(shù) 存在極值.…
存在極值.… 12分
12分
綜上所述:當(dāng)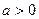 時,函數(shù)
時,函數(shù) 存在極值;當(dāng)
存在極值;當(dāng) 時,函數(shù)
時,函數(shù) 不存在極值.…14分
不存在極值.…14分
解法二:令 即
即 ,記
,記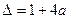
當(dāng) 即
即
 時,
時,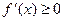 ,
, 在(0,+∞)單調(diào)遞增,無極值 ………9分
在(0,+∞)單調(diào)遞增,無極值 ………9分
當(dāng) 即
即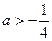 時,解
時,解 得:
得: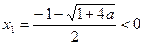 或
或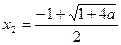
若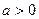 則
則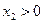 ,列表如下:
,列表如下: