【題目】一次數學測驗中，全班
名學生的數學成績的頻率分布直方圖如下，已知分數在
的學生數有14人.
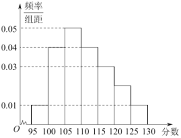
（1）求總人數和分數在
的人數
；
（2）利用頻率分布直方圖，估算該班學生數學成績的眾數和中位數，平均數各是多少？
【答案】（1）40，4
（2）眾數為107.5，中位數分別是110，平均數為111
【解析】
（1）先求出分數在
內的學生的頻率，根據頻率、頻數與總數之間的關系即可求得總人數，再計算分數在
內的學生的頻率，乘以總數即可得解；（2）眾數是最高的小矩形底邊中點的橫坐標，根據中位數左邊和右邊的直方圖面積相等可估計中位數，平均數的估計值等于頻率分布直方圖中每個小矩形的面積乘以小矩形底邊中點的橫坐標之和.
（1）分數在內的學生的頻率為
，
所以該班總人數為
.
分數在內的學生的頻率為：
，
分數在內的人數為
.
（2）由頻率直方圖可知眾數是最高的小矩形底邊中點的橫坐標，即為
.
設中位數為
，∵
，∴
.
∴眾數和中位數分別是107.5，110.
平均數為
.
科目：高中數學 來源： 題型：
【題目】（本小題滿分16分）設數列
的前n項和為
，數列
滿足:
,且數列的前
n項和為
.
(1) 求
的值；
(2) 求證：數列
是等比數列；
(3) 抽去數列中的第1項，第4項，第7項，……，第3n-2項，……余下的項順序不變，組成一個新數列
，若的前n項和為
，求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在多面體
中，
平面
，四邊形
為菱形，四邊形為梯形，且
，
，
，
，M為線段
的中點.
（1）求證：
平面
；
（2）求平面
將多面體分成的兩個部分的體積之比.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動點
到點
的距離，等于它到直線
的距離．
(1)求點的軌跡
的方程；
（2）過點
任意作互相垂直的兩條直線
，分別交曲線于點
和
．
設線段
，
的中點分別為
，求證：直線
恒過一個定點；
（3）在（2）的條件下，求
面積的最小值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，已知曲線
的參數方程為
（
， 
為參數）.以坐標原點
為極點， 
軸的正半軸為極軸，取相同的長度單位建立極坐標系，直線
的極坐標方程為
.
（Ⅰ）當
時，求曲線
上的點到直線
的距離的最大值；
（Ⅱ）若曲線
上的所有點都在直線
的下方，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分，（Ⅰ）小問6分，（Ⅱ）小問6分）一家公司計劃生產某種小型產品的月固定成本為
萬元，每生產萬件需要再投入
萬元.設該公司一個月內生產該小型產品
萬件并全部銷售完，每萬件的銷售收入為
萬元，且每萬件國家給予補助
萬元. （
為自然對數的底數，是一個常數.）
（Ⅰ）寫出月利潤
（萬元）關于月產量（萬件）的函數解析式；
（Ⅱ）當月生產量在
萬件時，求該公司在生產這種小型產品中所獲得的月利潤最大值（萬元）及此時的月生產量值（萬件）. （注：月利潤=月銷售收入+月國家補助-月總成本）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知兩個定點
，
， 動點
滿足
，設動點的軌跡為曲線
，直線
：
.
（1）求曲線的軌跡方程；
（2）若與曲線交于不同的
、
兩點，且
(
為坐標原點)，求直線的斜率；
（3）若
，
是直線上的動點，過作曲線的兩條切線
、
，切點為
、
，探究：直線
是否過定點，若存在定點請寫出坐標，若不存在則說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
