
【題目】已知橢圓![]() :
:![]() 與拋物線
與拋物線![]() 有公共的焦點
有公共的焦點![]() ,且公共弦長為
,且公共弦長為![]() ,
,
(1)求![]() ,
,![]() 的值.
的值.
(2)過![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,交
兩點,交![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() ,求
,求![]() .
.
 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,關于x的方程
,關于x的方程![]() ,下列四個結(jié)論中正確的有( )
,下列四個結(jié)論中正確的有( )
①存在實數(shù)k,使得方程恰有2個不同的實根;
②存在實數(shù)k,使得方程恰有4個不同的實根;
③存在實數(shù)k,使得方程恰有5個不同的實根;
④存在實數(shù)k,使得方程恰有8個不同的實根.
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】一次數(shù)學測驗中,全班![]() 名學生的數(shù)學成績的頻率分布直方圖如下,已知分數(shù)在
名學生的數(shù)學成績的頻率分布直方圖如下,已知分數(shù)在![]() 的學生數(shù)有14人.
的學生數(shù)有14人.
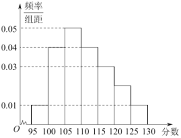
(1)求總?cè)藬?shù)![]() 和分數(shù)在
和分數(shù)在![]() 的人數(shù)
的人數(shù)![]() ;
;
(2)利用頻率分布直方圖,估算該班學生數(shù)學成績的眾數(shù)和中位數(shù),平均數(shù)各是多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列說法中,正確的有_______.
①回歸直線![]() 恒過點
恒過點![]() ,且至少過一個樣本點;
,且至少過一個樣本點;
②根據(jù)![]() 列列聯(lián)表中的數(shù)據(jù)計算得出
列列聯(lián)表中的數(shù)據(jù)計算得出![]() ,而
,而![]() ,則有99%的把握認為兩個分類變量有關系;
,則有99%的把握認為兩個分類變量有關系;
③![]() 是用來判斷兩個分類變量是否相關的隨機變量,當
是用來判斷兩個分類變量是否相關的隨機變量,當![]() 的值很小時可以推斷兩個變量不相關;
的值很小時可以推斷兩個變量不相關;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在P地正西方向8km的A處和正東方向1km的B處各有一條正北方向的公路AC和BD,現(xiàn)計劃在AC和BD路邊各修建一個物流中心E和F,為緩解交通壓力,決定修建兩條互相垂直的公路PE和PF,設![]()
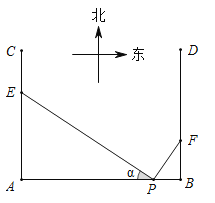
![]() Ⅰ
Ⅰ![]() 為減少對周邊區(qū)域的影響,試確定E,F的位置,使
為減少對周邊區(qū)域的影響,試確定E,F的位置,使![]() 與
與![]() 的面積之和最小;
的面積之和最小;
![]() Ⅱ
Ⅱ![]() 為節(jié)省建設成本,求使
為節(jié)省建設成本,求使![]() 的值最小時AE和BF的值.
的值最小時AE和BF的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某疾病控制中心為了研究某種病毒的抗體,將這種病毒感染源放人含40個小白鼠的封閉容器中進行感染,未感染病毒的小白鼠說明已經(jīng)產(chǎn)生了抗體,已知小白鼠對這種病毒產(chǎn)生抗體的概率為![]() .現(xiàn)對40個小白鼠進行抽血化驗,為了檢驗出所有產(chǎn)生該種病毒抗體的小白鼠,設計了下面的檢測方案:按
.現(xiàn)對40個小白鼠進行抽血化驗,為了檢驗出所有產(chǎn)生該種病毒抗體的小白鼠,設計了下面的檢測方案:按![]() (
(![]() ,且
,且![]() 是40的約數(shù))個小白鼠平均分組,并將抽到的同組的
是40的約數(shù))個小白鼠平均分組,并將抽到的同組的![]() 個小白鼠每個抽取的一半血混合在一起化驗,若發(fā)現(xiàn)該病毒抗體,則對該組的
個小白鼠每個抽取的一半血混合在一起化驗,若發(fā)現(xiàn)該病毒抗體,則對該組的![]() 個小白鼠抽取的另一半血逐一化驗,記
個小白鼠抽取的另一半血逐一化驗,記![]() 為某組中含有抗體的小白鼠的個數(shù).
為某組中含有抗體的小白鼠的個數(shù).
(1)若![]() ,求
,求![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
(2)為減少化驗次數(shù)的期望值,試確定![]() 的大小.
的大小.
(參考數(shù)據(jù):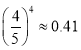 ,
,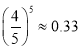 ,
,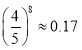 ,
, ,
,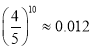 )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為了預防流感,某學校對教室用藥熏消毒法進行消毒.已知藥物釋放過程中,室內(nèi)每立方米空氣的含藥量![]() (毫克)與時間
(毫克)與時間![]() (小時)成正比.藥物釋放完畢后,
(小時)成正比.藥物釋放完畢后,![]() 與
與![]() 的函數(shù)關系式為
的函數(shù)關系式為![]() (
(![]() 為常數(shù)),如圖所示,根據(jù)圖中提供的信息,回答下列問題:
為常數(shù)),如圖所示,根據(jù)圖中提供的信息,回答下列問題:

(1)求從藥物釋放開始,每立方米空氣中的含藥量![]() (毫克)與時間
(毫克)與時間![]() (小時)之間的函數(shù)關系式;
(小時)之間的函數(shù)關系式;
(2)據(jù)測定,當空氣中每立方米空氣的含藥量降到0.25毫克以下時,學生方可進教室,那從藥物釋放開始,至少需要經(jīng)過多少小時后,學生才能回到進教室?
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com