Question

【題目】選修4-4：坐標系與參數方程

在極坐標系中，圓的極坐標方程為.若以極點為原點，極軸所在直線為軸建立平面直角坐標系.

（Ⅰ）求圓的參數方程；

（Ⅱ）在直角坐標系中，點是圓上動點，試求的最大值，并求出此時點的直角坐標.

Answer 1

【答案】（1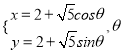）為參數（2）

【解析】試題分析：（Ⅰ）利用極坐標與直角坐標互化公式可得直角坐標方程，再利用同角三角函數的平方關系可得圓 的參數方程．
（Ⅱ）解法一：設，得代入

整理得，令。則問題得解

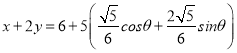解法二：由（Ⅰ）可得，設點 可得，可得 ，再利用三角函數的單調性與值域即可得出最大值．

試題解析：（Ⅰ）因為，所以，

即為圓C的普通方程．

所以所求的圓C的參數方程為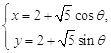(為參數)

（Ⅱ） 解法一：設，得代入整理得

(*)，則關于方程必有實數根

∴，化簡得

解得，即的最大值為11.

將代入方程(*)得，解得，代入得

故的最大值為11時，點的直角坐標為.

解法二：由（Ⅰ）可得，設點,

,

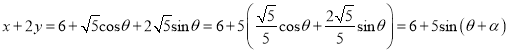其中，，當時，，

此時，,即，所以，

點的直角坐標為.