
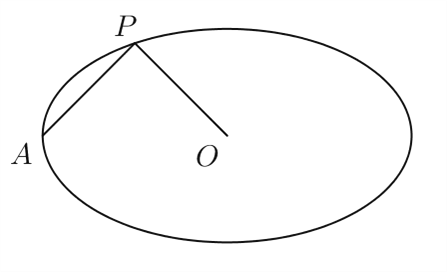
【題目】設橢圓M:![]() 的左頂點為
的左頂點為![]() 、中心為
、中心為![]() ,若橢圓M過點
,若橢圓M過點![]() ,且
,且![]()
![]() .
.
(1)求橢圓M的方程;
(2)若△APQ的頂點Q也在橢圓M上,試求△APQ面積的最大值;
(3)過點![]() 作兩條斜率分別為
作兩條斜率分別為![]() 的直線交橢圓M于
的直線交橢圓M于![]() 兩點,且
兩點,且![]() ,求證:直線
,求證:直線![]() 恒過一個定點.
恒過一個定點.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)由![]() ,可知
,可知![]() ,
,
又![]() 點坐標為
點坐標為![]() 故
故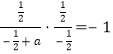 ,可得
,可得![]() ,
,
因為橢圓M過![]() 點,故
點,故![]() ,可得
,可得![]() ,
,
所以橢圓M的方程為![]() .
.
(2)AP的方程為![]() ,即
,即![]() ,
,
由于![]() 是橢圓M上的點,故可設
是橢圓M上的點,故可設![]() ,
,
所以![]()
![]()
當![]() ,即
,即![]() 時,
時,![]() 取最大值.
取最大值.
故![]() 的最大值為
的最大值為![]() .
.
法二:由圖形可知,若![]() 取得最大值,則橢圓在點
取得最大值,則橢圓在點![]() 處的切線
處的切線![]() 必平行于
必平行于![]() ,且在直線
,且在直線![]() 的下方.
的下方.
設![]() 方程為
方程為![]() ,代入橢圓M方程可得
,代入橢圓M方程可得![]() ,
,
由![]() ,可得
,可得![]() ,又
,又![]() ,故
,故![]() .
.
所以![]() 的最大值
的最大值![]() .
.
(3)直線![]() 方程為
方程為![]() ,代入
,代入![]() ,可得
,可得
![]() ,
,![]() ,
,
又![]() 故
故![]() ,
,![]() ,
,
同理可得![]() ,
,![]() ,又
,又![]() 且
且![]() ,可得
,可得![]() 且
且![]() ,
,
所以![]() ,
,![]() ,
,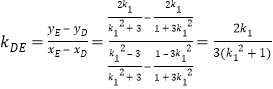 ,
,
直線![]() 的方程為
的方程為![]() ,
,
令![]() ,可得
,可得![]() .
.
故直線![]() 過定點
過定點![]() .
.
(法二)若![]() 垂直于
垂直于![]() 軸,則
軸,則![]() ,
,
此時![]() 與題設矛盾.
與題設矛盾.
若![]() 不垂直于
不垂直于![]() 軸,可設
軸,可設![]() 的方程為
的方程為![]() ,將其代入
,將其代入![]() ,
,
可得![]() ,可得
,可得![]() ,
,
又![]() ,
,
可得![]() ,
,
故![]() ,
,
可得![]() 或
或![]() ,又
,又![]() 不過
不過![]() 點,即
點,即![]() ,故
,故![]() .
.
所以![]() 的方程為
的方程為![]() ,故直線
,故直線![]() 過定點
過定點![]() .
.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:
【題目】已知動點![]() 到點
到點![]() 和直線l:
和直線l: ![]() 的距離相等.
的距離相等.
(Ⅰ)求動點![]() 的軌跡E的方程;
的軌跡E的方程;
(Ⅱ)已知不與![]() 垂直的直線
垂直的直線![]() 與曲線E有唯一公共點A,且與直線
與曲線E有唯一公共點A,且與直線![]() 的交點為
的交點為![]() ,以AP為直徑作圓
,以AP為直徑作圓![]() .判斷點
.判斷點![]() 和圓
和圓![]() 的位置關系,并證明你的結論.
的位置關系,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a∈R,函數f(x)=(﹣x2+ax)ex(x∈R,e為自然對數的底數).
(1)當a=2時,求函數f(x)的單調遞增區間;
(2)若函數f(x)在(﹣1,1)上單調遞增,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次小型抽獎活動中,抽獎規則如下:一個不透明的口袋中共有6個大小相同的球,它們是1個紅球,1個黃球,和4個白球,從中抽到紅球中50元,抽到黃球中10元,抽到白球不中獎.某人從中一次性抽出兩球,求:
(1)該人中獎的概率;
(2)該人獲得的總獎金X(元)的分布列和均值E(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,已知AC⊥BC,BC=CC1 , 設AB1的中點為D,B1C∩BC1=E. 
求證:
(1)DE∥平面AA1C1C;
(2)BC1⊥AB1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線的方程為![]() ,過點
,過點![]() 的一條直線與拋物線
的一條直線與拋物線![]() 交于
交于![]() 兩點,若拋物線在
兩點,若拋物線在![]() 兩點的切線交于點
兩點的切線交于點![]() .
.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設直線![]() 與直線
與直線![]() 的夾角為
的夾角為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}是等差數列,滿足a1=3,a4=12,數列{bn}滿足b1=4,b4=20,且{bn﹣an}為等比數列.
(1)求數列{an}和{bn}的通項公式;
(2)求數列{bn}的前n項和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com