【題目】已知函數
， 
是函數
的極值點.
（1）若
，求函數
的最小值；
（2）若
不是單調函數，且無最小值，證明： 
.
【答案】（1）
的最小值為
；（2）見解析.
【解析】試題分析：（1）
在區間
單調遞減，在
上單調遞增，所以
的最小值為
；（2）
，方程
（
），
不是單調函數，且無最小值，則方程
必有
個不相等的正根， 
是極大值點， 
是極小值點， 
，只需證明
。
試題解析：
（1）解： 
，其定義域是
.
.
令
，得
所以， 
在區間
單調遞減，在
上單調遞增.
所以
的最小值為
.
（2）解：函數
的定義域是
對
求導數，得
顯然，方程
（
）
設
不是單調函數，且無最小值，則方程
必有
個不相等的正根，所以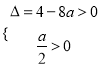
解得
設方程
的
個不相等的正根是
， 
，其中
所以
列表分析如下：
|
|
|
|
|
|
|
|
|
|
|
|
所以， 
是極大值點， 
是極小值點， 
故只需證明
，由
，且
得
因為
， 
，所以
從而
名校課堂系列答案科目：高中數學 來源： 題型：
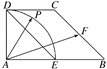
【題目】(2016·沈陽期中)在直角梯形ABCD中，AB⊥AD，DC∥AB，AD＝DC＝1，AB＝2，E、F分別為AB、BC的中點，點P在以A為圓心，AD為半徑的圓弧
上變動(如圖所示)．若
＝λ
＋μ
，其中λ，μ∈R，則2λ－μ的取值范圍是______________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已經函數
的定義域為
，設
（1）試確定
的取值范圍，使得函數
在
上為單調函數
（2）求證
（3）若不等式
（為
正整數）對任意正實數
恒成立，求
的最大值.（解答過程可參考使用以下數據
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】第三屆移動互聯創新大賽，于2017年3月～10月期間舉行，為了選出優秀選手，某高校先在計算機科學系選出一種子選手
，再從全校征集出3位志愿者分別與
進行一場技術對抗賽，根據以往經驗， 
與這三位志愿者進行比賽一場獲勝的概率分別為
，且各場輸贏互不影響.
（1）求甲恰好獲勝兩場的概率；
（2）求甲獲勝場數的分布列與數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
，圓
，點
是圓上一動點， 
的垂直平分線與線段
交于點
.
（1）求點
的軌跡方程；
（2）設點
的軌跡為曲線
，過點
且斜率不為0的直線
與
交于
兩點，點
關于
軸的對稱點為
，證明直線
過定點，并求
面積的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
是自然對數的底數）
（1）若直線
為曲線
的一條切線，求實數
的值；
（2）若函數
在區間
上為單調函數，求實數
的取值范圍；
（3）設
，若
在定義域上有極值點（極值點是指函數取得極值時對應的自變量的值），求實數
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
