
【題目】過拋物線y2=4x的焦點F的直線交拋物線于A、B兩點,分別過A、B兩點作準線的垂線,垂足分別為A′、B′兩點,以線段A′B′為直徑的圓C過點(﹣2,3),則圓C的方程為( )
A.(x+1)2+(y﹣2)2=2
B.(x+1)2+(y﹣1)2=5
C.(x+1)2+(y+1)2=17
D.(x+1)2+(y+2)2=26
 名師點撥卷系列答案
名師點撥卷系列答案科目:高中數學 來源: 題型:
【題目】某重點中學將全部高一學生分成![]() 兩個成績相當(成績的均值、方差都相同)的級部,
兩個成績相當(成績的均值、方差都相同)的級部, ![]() 級部采用傳統形式的教學方式,
級部采用傳統形式的教學方式, ![]() 級部采用新型的基于信息化的自主學習教學方式.為了解教學效果,期末考試后分別從兩個級部中各隨機抽取30名學生的數學成績進行統計,做出莖葉圖如下,記成績不低于127分者為“優秀”.
級部采用新型的基于信息化的自主學習教學方式.為了解教學效果,期末考試后分別從兩個級部中各隨機抽取30名學生的數學成績進行統計,做出莖葉圖如下,記成績不低于127分者為“優秀”.
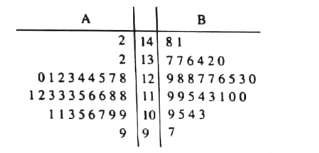
(1)在![]() 級部樣本的30個個體中隨機抽取1個,求抽出的為“優秀”的概率;
級部樣本的30個個體中隨機抽取1個,求抽出的為“優秀”的概率;
(2)由以上數據填寫下面列聯表,并判斷是否有![]() 的把握認為“優秀”與教學方式有關.
的把握認為“優秀”與教學方式有關.
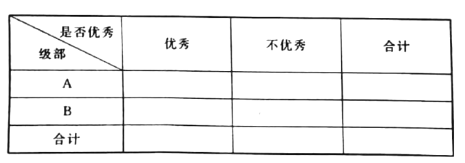
附表:

附: 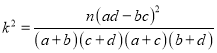 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是正方體的平面展開圖,在這個正方體中
(1)BM與ED平行 (2)CN與BE是異面直線
(3)CN與BM成60° (4)DM與BN垂直
以上四個命題中,正確命題的序號是( )
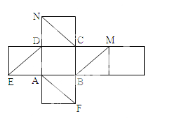
A. (1)(2)(3) B. (2)(4) C. (3)(4) D. (2)(3)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,橢圓
上,橢圓![]() 的四個頂點的連線構成的四邊形的面積為
的四個頂點的連線構成的四邊形的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 為橢圓長軸的左端點,
為橢圓長軸的左端點, ![]() 為橢圓上異于橢圓
為橢圓上異于橢圓![]() 長軸端點的兩點,記直線
長軸端點的兩點,記直線![]() 斜率分別為
斜率分別為![]() 、
、![]() ,若
,若![]() ,請判斷直線
,請判斷直線![]() 是否過定點?若過定點,求該定點坐標,若不過定點,請說明理由.
是否過定點?若過定點,求該定點坐標,若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
.
(1)求函數![]() 的最小正周期;
的最小正周期;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]()
【解析】試題分析:(1)根據二倍角公式和兩角和差公式得到![]() ,進而得到周期;(2)由
,進而得到周期;(2)由![]() ,得到
,得到![]() ,
, ![]() ,由配湊角公式得到
,由配湊角公式得到![]() ,代入值得到函數值.
,代入值得到函數值.
解析:
(1)由題意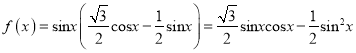
![]() =
=![]()
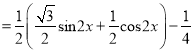
![]()
所以![]() 的最小正周期為
的最小正周期為![]() ;
;
(2)由![]()
![]()
又由![]() 得
得![]() ,所以
,所以![]()
故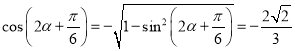 ,
,
故![]()
![]()
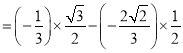
![]()
【題型】解答題
【結束】
20
【題目】為響應十九大報告提出的實施鄉村振興戰略,某村莊投資![]() 萬元建起了一座綠色農產品加工廠.經營中,第一年支出
萬元建起了一座綠色農產品加工廠.經營中,第一年支出![]() 萬元,以后每年的支出比上一年增加了
萬元,以后每年的支出比上一年增加了![]() 萬元,從第一年起每年農場品銷售收入為
萬元,從第一年起每年農場品銷售收入為![]() 萬元(前
萬元(前![]() 年的純利潤綜合=前
年的純利潤綜合=前![]() 年的 總收入-前
年的 總收入-前![]() 年的總支出-投資額
年的總支出-投資額![]() 萬元).
萬元).
(1)該廠從第幾年開始盈利?
(2)該廠第幾年年平均純利潤達到最大?并求出年平均純利潤的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() ,
, ![]() ,其離心率為
,其離心率為![]() ,短軸端點與焦點構成四邊形的面積為
,短軸端點與焦點構成四邊形的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,
, ![]() 為坐標原點,當
為坐標原點,當![]() 時,試求直線
時,試求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知圓O1與圓O2相交于A,B兩點,過點A作圓O1的切線交圓O2于點C,過點B作兩圓的割線,分別交圓O1 , 圓O2于點D,E,DE與AC相交于點P. 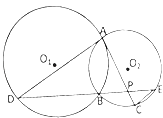
(1)求證:AD∥EC;
(2)若AD是圓O2的切線,且PA=3,PC=1,AD=6,求DB的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,給出下列結論:
,給出下列結論:
(1)若對任意![]() ,且
,且![]() ,都有
,都有![]() ,則
,則![]() 為R上減函數;
為R上減函數;
(2) 若![]() 為R上的偶函數,且在
為R上的偶函數,且在![]() 內是減函數,
內是減函數, ![]() (-2)=0,則
(-2)=0,則![]() >0解集為(-2,2);
>0解集為(-2,2);
(3)若![]() 為R上的奇函數,則
為R上的奇函數,則![]() 也是R上的奇函數;
也是R上的奇函數;
(4)若一個函數定義域![]() 且
且![]() 的奇函數,當
的奇函數,當![]() 時,
時,![]() ,則當x<0時
,則當x<0時![]() ,其中正確的是____________________
,其中正確的是____________________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com