【題目】人的正常體溫在
至
之間，下圖是一位病人在治療期間的體溫變化圖.
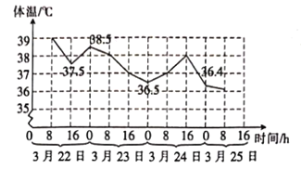
現有下述四個結論：
①此病人已明顯好轉；
②治療期間的體溫極差小于
；
③從每8小時的變化來看，25日0時~8時體溫最穩定；
④從3月22日8時開始，每8小時量一次體溫，若體溫不低于
就服用退燒藥，根據圖中信息可知該病人服用了3次退燒藥.
其中所有正確結論的編號是（ ）
A.③④B.②③C.①②④D.①②③
科目：高中數學 來源： 題型：
【題目】有2002名運動員，號碼依次為
．從中選出若干名運動員參加儀仗隊，但要使剩下的運動員中沒有一個人的號碼數等于另外兩人的號碼數的乘積．那么，被選為儀仗隊的運動員至少能有多少人？給出你的選取方案，并簡述理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在一個十進制正整數中，如果它含有偶數（包括零）個數字 8 ，則稱它為“優數” ，否則就稱它為“非優數” .那么，長度（位數）不超過
（是正整數）的所有“優數” 的個數是 __________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某書店剛剛上市了《中國古代數學史》，銷售前該書店擬定了5種單價進行試銷，每種單價（
元）試銷l天，得到如表單價（元）與銷量
（冊）數據：
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
（l）根據表中數據，請建立關于的回歸直線方程：
（2）預計今后的銷售中，銷量（冊）與單價（元）服從（l）中的回歸方程，已知每冊書的成本是12元，書店為了獲得最大利潤，該冊書的單價應定為多少元？
附：
，
，
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，已知點
，曲線
的參數方程為
（
為參數），點
是曲線上的任意一點，點
為
的中點，以坐標原點為極點，
軸的正半軸為極軸建立極坐標系.
（1）求點的軌跡
的極坐標方程；
（2）已知直線
：
與曲線交于點
，
，射線
逆時針旋轉
交曲線于點
，且
，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某家庭進行理財投資，根據長期收益率市場預測，投資債券等穩健型產品的收益
與投資額
成正比，且投資1萬元時的收益為
萬元，投資股票等風險型產品的收益
與投資額的算術平方根成正比，且投資1萬元時的收益為0.5萬元，
（1）分別寫出兩種產品的收益與投資額的函數關系；
（2）該家庭現有20萬元資金，全部用于理財投資，問：怎樣分配資金能使投資獲得最大收益，其最大收益為多少萬元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨機抽取某校高一100名學生的期末考試英語成績（他們的英語成績都在80分
140分之間），將他們的英語成績（單位：分）分成：
，
，
，
，
六組，得到如圖所示的部分頻率分布直方圖，已知成績處于內與內的頻數之和等于成績處于
內的頻數，根據圖中的信息，回答下列問題：
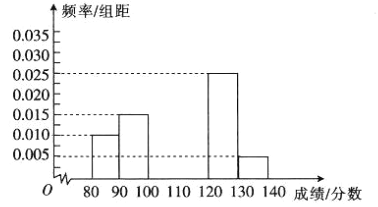
（1）求頻率分布直方圖中未畫出的小矩形的面積之和；
（2）求成績處于內與內的頻率之差；
（3）用分層抽樣的方法從成績不低于120分的學生中選取一個容量為6的樣本，將該樣本看成一個總體，從中任選2人，求這2人中恰有一人成績低于130分的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平行六面體ABCD—A1B1C1D1中，AB＝AC，平面BB1C1C⊥底面ABCD，點M、F分別是線段AA1、BC的中點．
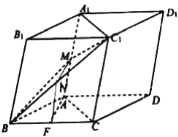
（1）求證：AF⊥DD1；
（2）求證：AF∥平面MBC1．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
