
【題目】在平面直角坐標系![]() 中,點
中,點![]() 、
、![]() 、
、![]() .
.
(1)求以線段![]() 、
、![]() 為鄰邊的平行四邊形兩條對角線的長;
為鄰邊的平行四邊形兩條對角線的長;
(2)設![]() ,且
,且![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() 、
、![]() ;(2)
;(2)![]() .
.
【解析】
(1)方法一:計算出向量![]() 、
、![]() ,利用平面向量的坐標運算可求出所求得的兩條對角線
,利用平面向量的坐標運算可求出所求得的兩條對角線![]() 和
和![]() 的長度;
的長度;
方法二:利用平行四邊形的對角線互相平分可求出第四個頂點![]() 的坐標,然后利用兩點間的距離公式可求得平行四邊形兩條對角線的長度;
的坐標,然后利用兩點間的距離公式可求得平行四邊形兩條對角線的長度;
(2)求出向量![]() 的坐標,然后利用共線向量的坐標表示可得出關于實數
的坐標,然后利用共線向量的坐標表示可得出關于實數![]() 的方程,解出即可.
的方程,解出即可.
(1)(方法一)由題設知![]() ,
,![]() ,
,
則![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
故所求的兩條對角線的長分別為![]() 、
、![]() ;
;
(方法二)設該平行四邊形的第四個頂點為![]() ,兩條對角線的交點為
,兩條對角線的交點為![]() ,
,
則![]() 為
為![]() 、
、![]() 的中點,
的中點,![]() ,
,
又![]() 為
為![]() 的中點,則
的中點,則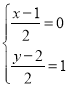 ,解得
,解得![]() ,則點
,則點![]() ,
,
由兩點間的距離公式可得![]() ,
,
![]() ,
,
故所求的兩條對角線的長分別為![]() 、
、![]() ;
;
(2)由題設知:![]() ,
,![]() .
.
由![]() ,得
,得![]() ,從而
,從而![]() ,所以
,所以![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數 和
和![]() (
(![]() 且為常數),則下列結論正確的是( )
且為常數),則下列結論正確的是( )
A.當![]() 時,存在實數
時,存在實數![]() ,使得關于
,使得關于![]() 的方程
的方程![]() 有四個不同的實數根
有四個不同的實數根
B.存在![]() ,使得關于
,使得關于![]() 的方程
的方程![]() 有三個不同的實數根
有三個不同的實數根
C.當![]() 時,若函數
時,若函數![]() 恰有
恰有![]() 個不同的零點
個不同的零點![]() 、
、![]() 、
、![]() ,則
,則![]()
D.當![]() 時,且關于
時,且關于![]() 的方程
的方程![]() 有四個不同的實數根
有四個不同的實數根![]() 、
、![]() 、
、![]() 、
、![]()
![]() ,若
,若![]() 在
在![]() 上的最大值為
上的最大值為![]() ,則
,則![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某區組織部為了了解全區科級干部“黨風廉政知識”的學習情況,按照分層抽樣的方法,從全區320名正科級干部和1280名副科級干部中抽取40名科級干部預測全區科級干部“黨風廉政知識”的學習情況.現將這40名科級干部分為正科級干部組和副科級干部組,利用同一份試卷分別進行預測.經過預測后,兩組各自將預測成績統計分析如下表:
分組 | 人數 | 平均成績 | 標準差 |
正科級干部組 |
| 80 | 6 |
副科級干部組 |
| 70 | 4 |
(1)求![]() ;
;
(2)求這40名科級干部預測成績的平均分![]() 和標準差
和標準差![]() ;
;
(3)假設該區科級干部的“黨風廉政知識”預測成績服從正態分布![]() ,用樣本平均數
,用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,用樣本標準差
,用樣本標準差![]() 作為
作為![]() 的估計值
的估計值![]() .利用估計值估計:該區科級干部“黨風廉政知識”預測成績小于60分的約為多少人?
.利用估計值估計:該區科級干部“黨風廉政知識”預測成績小于60分的約為多少人?
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)計算![]() ,
,![]() ,
,![]() ,
,![]() ,并求數列
,并求數列![]() 的通項公式;
的通項公式;
(2)若數列![]() 滿足
滿足![]() ,求證:數列
,求證:數列![]() 是等比數列;
是等比數列;
(3)由數列![]() 的項組成一個新數列
的項組成一個新數列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,設
,設![]() 為數列
為數列![]() 的前
的前![]() 項和,試求
項和,試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙二人用4張撲克牌(分別是紅桃2,紅桃3,紅桃4,方片4)完游戲,他們將撲克牌洗勻后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一張.
(1)設![]() 分別表示甲、乙抽到的牌的數字,寫出甲乙二人抽到的牌的所有情況;
分別表示甲、乙抽到的牌的數字,寫出甲乙二人抽到的牌的所有情況;
(2)若甲抽到紅桃3,則乙抽出的牌的牌面數字比3大的概率是多少?
(3)甲乙約定:若甲抽到的牌的牌面數字比乙大,則甲勝,反之,則乙勝,你認為此游戲是否公平,說明你的理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某兒童玩具生產廠一車間計劃每天生產遙控小車模型、遙控飛機模型、遙控火車模型這三種玩具共![]() 個,生產一個遙控小車模型需
個,生產一個遙控小車模型需![]() 分鐘,生產一個遙控飛機模型需
分鐘,生產一個遙控飛機模型需![]() 分鐘,生產一個遙控火車模型需
分鐘,生產一個遙控火車模型需![]() 分鐘,已知總生產時間不超過
分鐘,已知總生產時間不超過![]() 分鐘,若生產一個遙控小車模型可獲利
分鐘,若生產一個遙控小車模型可獲利![]() 元,生產一個遙控飛機模型可獲利
元,生產一個遙控飛機模型可獲利![]() 元,生產一個遙控火車模型可獲利
元,生產一個遙控火車模型可獲利![]() 元,該公司合理分配生產任務可使每天的利潤最大,則最大利潤是__________元
元,該公司合理分配生產任務可使每天的利潤最大,則最大利潤是__________元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com