
【題目】已知橢圓 ![]() 的一個頂點為A(2,0),離心率為
的一個頂點為A(2,0),離心率為 ![]() .直線y=k(x-1)與橢圓C交于不同的兩點M、N.
.直線y=k(x-1)與橢圓C交于不同的兩點M、N.
(1)求橢圓C的方程.
(2)當△AMN的面積為 ![]() 時,求k的值.
時,求k的值.
【答案】
(1)解:由題意得 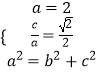 ,解得
,解得 ![]() ,所以橢圓C的方程為
,所以橢圓C的方程為 ![]()
(2)解:由 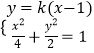 ,得
,得 ![]() ,
,
設點M、N的坐標分別為 ![]() ,則
,則 ![]() ,
, ![]() ,
, ![]() , 所以
, 所以![]()
![]()
![]()
又因為點 ![]() 到直線
到直線 ![]() 的距離
的距離 ![]() ,所以
,所以 ![]() 的面積為
的面積為 ![]() ,
,
由 ![]() 得,
得, ![]()
【解析】(1)運用離心率公式和a,b,c的關系,解得b,進而得到橢圓方程;
(2)聯立直線方程和橢圓方程,消去y,運用韋達定理和配方,化簡整理,解方程即可得到k.本題考查了橢圓的標準方程及其性質、直線與橢圓相交弦長問題、三角形面積計算公式、點到直線的距離公式,考查了推理能力與計算能力,屬于中檔題.
【考點精析】根據題目的已知條件,利用橢圓的標準方程的相關知識可以得到問題的答案,需要掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() .
.


科目:高中數學 來源: 題型:
【題目】70年代中期,美國各所名牌大學校園內,人們都像發瘋一般,夜以繼日,廢寢忘食地玩一個數學游戲.這個游戲十分簡單:任意寫出一個自然數N,并且按照以下的規律進行變換:如果是個奇數,則下一步變成3N+1;如果是個偶數,則下一步變成 ![]() .不單單是學生,甚至連教師、研究員、教授與學究都紛紛加入.為什么這個游戲的魅力經久不衰?因為人們發現,無論N是怎樣一個數字,最終都無法逃脫回到谷底1.準確地說,是無法逃出落入底部的4﹣2﹣1循環,永遠也逃不出這樣的宿命.這就是著名的“冰雹猜想”.按照這種運算,自然數27經過十步運算得到的數為( )
.不單單是學生,甚至連教師、研究員、教授與學究都紛紛加入.為什么這個游戲的魅力經久不衰?因為人們發現,無論N是怎樣一個數字,最終都無法逃脫回到谷底1.準確地說,是無法逃出落入底部的4﹣2﹣1循環,永遠也逃不出這樣的宿命.這就是著名的“冰雹猜想”.按照這種運算,自然數27經過十步運算得到的數為( )
A.142
B.71
C.214
D.107
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 過圓
過圓![]() 與直線
與直線![]() 的交點,且圓
的交點,且圓![]() 上任意一點關于直線
上任意一點關于直線![]() 的對稱點仍在圓
的對稱點仍在圓![]() 上.
上.
(1)求圓![]() 的標準方程;
的標準方程;
(2)若圓![]() 與
與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,直線
,直線![]() 與圓
與圓![]() 交于
交于![]() 兩點(異于點
兩點(異于點![]() ),且點
),且點![]() 滿足
滿足![]() ,
,![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線 ![]() 的焦點為
的焦點為 ![]() ,
, ![]() 是拋物線上橫坐標為4,且位于
是拋物線上橫坐標為4,且位于 ![]() 軸上方的點,
軸上方的點, ![]() 到拋物線準線的距離等于5,過
到拋物線準線的距離等于5,過 ![]() 作
作 ![]() 垂直于
垂直于 ![]() 軸,垂足為
軸,垂足為 ![]() ,
, ![]() 的中點為
的中點為 ![]() .
.
(1)求拋物線的方程;
(2)若過 ![]() 作
作 ![]() ,垂足為
,垂足為 ![]() ,求點
,求點 ![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)求函數f(x)的單調區間;
(2)當a≠0時,過原點分別作曲線y=f(x)與y=g(x)的切線l1 , l2 , 已知兩切線的斜率互為倒數,證明: ![]() <a<
<a< ![]() ;
;
(3)設h(x)=f(x+1)+g(x),當x≥0,h(x)≥1時,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學著作《九章算術》有如下問題:“今有蒲(水生植物名)生一日,長三尺;莞(植物名,俗稱水蔥、席子草)生一日,長一尺.蒲生日自半,莞生日自倍.問幾何日而長等?”意思是:今有蒲生長1日,長為3尺;莞生長1日,長為1尺.蒲的生長逐日減半,莞的生長逐日增加1倍.若蒲、莞長度相等,則所需的時間約為日.(結果保留一位小數,參考數據:lg2≈0.30,lg3≈0.48)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題:(1)已知向量 ![]() 是空間的一組基底,則向量
是空間的一組基底,則向量 ![]() 也是空間的一組基底;(2) 在正方體
也是空間的一組基底;(2) 在正方體 ![]() 中,若點
中,若點 ![]() 在
在 ![]() 內,且
內,且 ![]() ,則
,則 ![]() 的值為1;(3) 圓
的值為1;(3) 圓 ![]() 上到直線
上到直線 ![]() 的距離等于1的點有2個;(4)方程
的距離等于1的點有2個;(4)方程 ![]() 表示的曲線是一條直線.其中正確命題的序號是.
表示的曲線是一條直線.其中正確命題的序號是.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產某種產品,每生產1噸產品需人工費4萬元,每天還需固定成本3萬元.經過長期調查統計,每日的銷售額![]() (單位:萬元)與日產量
(單位:萬元)與日產量![]() (單位:噸)滿足函數關系
(單位:噸)滿足函數關系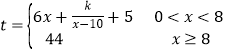 ,已知每天生產4噸時利潤為7萬元.
,已知每天生產4噸時利潤為7萬元.
(1)求![]() 的值;
的值;
(2)當日產量為多少噸時,每天的利潤最大,最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】潮州統計局就某地居民的月收入調查了![]() 人,并根據所得數據畫了樣本的頻率分
人,并根據所得數據畫了樣本的頻率分
布直方圖(每個分組包括左端點,不包括右端點,如第一組表示收入在![]() )。
)。

(1)求居民月收入在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析居民的收入與年齡、職業等方面的關系,必須按月收入再從這![]() 人中分層抽樣方法抽出
人中分層抽樣方法抽出![]() 人作進一步分析,則月收入在
人作進一步分析,則月收入在![]() 的這段應抽多少人?
的這段應抽多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com