
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若![]() 只有一個零點
只有一個零點![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根據(jù)導數(shù)的幾何意義求出切線的斜率,然后由點斜式可得所求切線方程.(2)利用導數(shù)判斷出函數(shù)![]() 的單調性和極值,進而得到函數(shù)
的單調性和極值,進而得到函數(shù)![]() 的大體圖象,然后根據(jù)函數(shù)的圖象及極值判斷出函數(shù)只有一個零點時參數(shù)
的大體圖象,然后根據(jù)函數(shù)的圖象及極值判斷出函數(shù)只有一個零點時參數(shù)![]() 的取值范圍.
的取值范圍.
(1)當![]() 時,
時,![]() ,
,
所以![]() ,
,
故![]() ,
,
又![]() ,
,
所以曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,
,
即![]() .
.
(2)由題意得![]() .
.
(i)當![]() ,即
,即![]() 時,
時,
則當![]() 或
或![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以![]() 的極小值為
的極小值為![]() ,
,
因為函數(shù)的零點![]() ,且
,且![]() ,
,
所以當函數(shù)只有一個零點時,需滿足![]() ,
,
又![]() ,則
,則![]() 或
或![]() .
.
(ii)當![]() ,即
,即![]() 時,則有
時,則有![]() ,
,
所以![]() 為增函數(shù).
為增函數(shù).
又![]() ,
,
所以![]() 只有一個零點
只有一個零點![]() ,且
,且![]() ,
,
所以![]() 滿足題意.
滿足題意.
(iii)當![]() ,即
,即![]() 時,
時,
則當![]() 或
或![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() .
.
所以![]() 的極小值為
的極小值為![]() ,極大值為
,極大值為![]() ,
,
因為![]() ,
,![]() ,
,
所以![]() ,
,
又![]() ,所以
,所以![]() .
.
綜上可得![]() 或
或![]() .
.
實數(shù)![]() 的取值范圍為
的取值范圍為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系xOy中,以O為極點,x軸正半軸為極軸建立極坐標系.已知曲線C的極坐標方程為ρ(1-cos2θ)=8cosθ,直線ρcosθ=1與曲線C相交于M,N兩點,直線l過定點P(2,0)且傾斜角為α,l交曲線C于A,B兩點.
(1)把曲線C化成直角坐標方程,并求|MN|的值;
(2)若|PA|,|MN|,|PB|成等比數(shù)列,求直線l的傾斜角α.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,平面![]() 平面
平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四邊形
,四邊形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.
的中點.
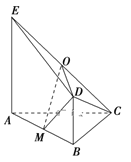
(1求異面直角![]() 與
與![]() 所成角的大小;
所成角的大小;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,左焦點為
,左焦點為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上位于
上位于![]() 軸上方的一個動點,當直線
軸上方的一個動點,當直線![]() 的斜率為1時,
的斜率為1時,![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 的另外一個交點為
的另外一個交點為![]() ,點
,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為降低汽車尾氣排放量,某工廠設計制造了![]() 、
、![]() 兩種不同型號的節(jié)排器,規(guī)定性能質量評分在
兩種不同型號的節(jié)排器,規(guī)定性能質量評分在![]() 的為優(yōu)質品.現(xiàn)從該廠生產的
的為優(yōu)質品.現(xiàn)從該廠生產的![]() 、
、![]() 兩種型號的節(jié)排器中,分別隨機抽取500件產品進行性能質量評分,并將評分分別分成以下六個組;
兩種型號的節(jié)排器中,分別隨機抽取500件產品進行性能質量評分,并將評分分別分成以下六個組;![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,繪制成如圖所示的頻率分布直方圖:
,繪制成如圖所示的頻率分布直方圖:
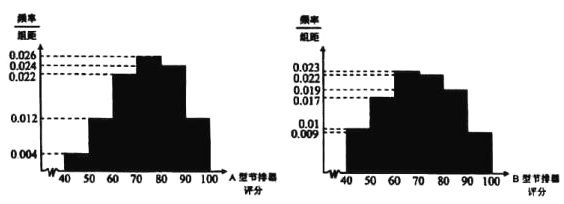
(1)設500件![]() 型產品性能質量評分的中位數(shù)為
型產品性能質量評分的中位數(shù)為![]() ,直接寫出
,直接寫出![]() 所在的分組區(qū)間;
所在的分組區(qū)間;
(2)請完成下面的列聯(lián)表(單位:件)(把有關結果直接填入下面的表格中);
|
| 總計 | |
優(yōu)質品 | |||
非優(yōu)質品 | |||
總計 | 500 | 500 | 1000 |
(3)根據(jù)(2)中的列聯(lián)表,能否有![]() 的把握認為
的把握認為![]() 、
、![]() 兩種不同型號的節(jié)排器性能質量有差異?
兩種不同型號的節(jié)排器性能質量有差異?
附:![]() ,其中
,其中![]() .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
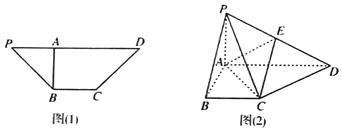
【題目】如圖![]() 在四邊形PBCD中,
在四邊形PBCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,沿AB把三角形PAB折起,使P,D兩點的距離為10,得到如圖
,沿AB把三角形PAB折起,使P,D兩點的距離為10,得到如圖![]() 所示圖形.
所示圖形.
![]() Ⅰ
Ⅰ![]() 求證:平面
求證:平面![]() 平面PAC;
平面PAC;
![]() Ⅱ
Ⅱ![]() 若點E是PD的中點,求三棱錐
若點E是PD的中點,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com