Question

【題目】現如今，“網購”一詞不再新鮮，越來越多的人已經接受并喜歡了這種購物方式，但隨之也出現了商品質量不能保證與信譽不好等問題，因此，相關管理部門制定了針對商品質量與服務的評價體系，現從評價系統中選出成功交易200例，并對其評價進行統計：對商品的好評率為0.6，對服務的好評率為0.75，其中對商品和服務都做出好評的交易為80次.

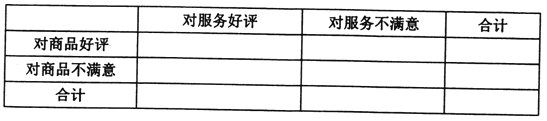
（1）依據題中的數據完成下表，并通過計算說明，能否有99.9%的把握認為“商品好評與服務好評”有關；

（2）若將頻率視為概率，某人在該購物平臺上進行了5次購物，設對商品和服務全好評的次數為隨機變量，求的分布列（概率用算式表示）、數學期望和方差.

Answer 1

【答案】（Ⅰ）有%的把握（Ⅱ），

【解析】試題分析：（1）利用樣本乘以商品好評率得到好評人數，用樣本乘以服務好評率得到對服務滿意人數，由此填寫聯表，計算出，故有的把握認為“商品好評和服務好評”有關.（2）對商品和服務都好評的概率為， 次購物相當于的獨立重復試驗，故利用二項分布來計算分布列、期望和方程.

試題解析：

（1） 根據題中條件可得關于商品和服務的列聯表：

		對服務好評		對服務不滿意		合計
對商品好評
對商品不滿意
合計

因此，有%的把握認為“商品好評與服務好評”有關.

（2）由題可得，每次購物時，對商品和服務都好評的概率為

的所有可能的取值為，則～，

所以， ， ，

， ，

分布列為：

由于～，

所以，