
【題目】[選修4-4:坐標系與參數方程]
已知在直角坐標系xOy中,曲線C的參數方程為 ![]() (φ為參數),在極坐標系(與直角坐標系xOy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,直線l的方程為ρcos(θ﹣
(φ為參數),在極坐標系(與直角坐標系xOy取相同的長度單位,且以原點O為極點,以x軸正半軸為極軸)中,直線l的方程為ρcos(θ﹣ ![]() )=2
)=2 ![]() .
.
(Ⅰ)求曲線C在極坐標系中的方程;
(Ⅱ)求直線l被曲線C截得的弦長.
 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在多面體ABCDEF中,四邊形ABCD為邊長為4的正方形,M是BC的中點,EF∥平面ABCD,且EF=2,AE=DE=BF=CF= ![]() .
. 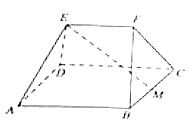
(1)求證:ME⊥平面ADE;
(2)求二面角B﹣AE﹣D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣ ![]() ﹣2lnx,a∈R.
﹣2lnx,a∈R.
(1)討論函數f(x)的單調性;
(2)若函數f(x)有兩個極值點x1 , x2 , 且x1<x2 , 求a的取值范圍;
(3)在(2)的條件下,證明:f(x2)<x2﹣1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》第三章“衰分”介紹比例分配問題:“衰分”是按比例遞減分配的意思,通常稱遞減的比例(百分比)為“衰分比”.如:甲、乙、丙、丁衰分得100,60,36,21.6個單位,遞減的比例為40%,今共有糧m(m>0)石,按甲、乙、丙、丁的順序進行“衰分”,已知丙衰分得80石,乙、丁衰分所得的和為164石,則“衰分比”與m的值分別為( )
A.20% 369
B.80% 369
C.40% 360
D.60% 365
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是線段BF上一點,AB=AF=BC.
2CE,G是線段BF上一點,AB=AF=BC. 
(Ⅰ)若EG∥平面ABC,求 ![]() 的值;
的值;
(Ⅱ)求二面角A﹣BF﹣E的大小的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,點O為數軸的原點,A,B,M為數軸上三點,C為線段OM上的動點.設x表示點C與原點的距離,y表示點C到點A的距離的4倍與點C到點B的距離的6倍之和.
![]()
(1)將y表示為x的函數;
(2)要使y的值不超過70,實數x應該在什么范圍內取值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在正方形ABCD中,點E,F分別是AB,BC的中點,BD與EF交于點H,G為BD中點,點R在線段BH上,且 ![]() =λ(λ>0).現將△AED,△CFD,△DEF分別沿DE,DF,EF折起,使點A,C重合于點B(該點記為P),如圖2所示.
=λ(λ>0).現將△AED,△CFD,△DEF分別沿DE,DF,EF折起,使點A,C重合于點B(該點記為P),如圖2所示. 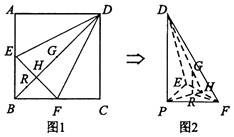
(I)若λ=2,求證:GR⊥平面PEF;
(Ⅱ)是否存在正實數λ,使得直線FR與平面DEF所成角的正弦值為 ![]() ?若存在,求出λ的值;若不存在,請說明理由.
?若存在,求出λ的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com