
【題目】在△ABC中,A、B、C的對邊分別為a、b、c,己知c﹣b=2bcosA.
(1)若a=2 ![]() ,b=3,求c;
,b=3,求c;
(2)若C= ![]() ,求角B.
,求角B.
【答案】
(1)解:∵c﹣b=2bcosA.
∴由余弦定理可得:c﹣b=2b× ![]() ,整理可得:a2=b2+bc,
,整理可得:a2=b2+bc,
∵a=2 ![]() ,b=3,
,b=3,
∴24=9+3c,解得:c=5.
(2)解:∵C= ![]() ,∴A+B=
,∴A+B= ![]() ,可得sinA=cosB,cosA=sinB,
,可得sinA=cosB,cosA=sinB,
∴c﹣b=2bcosA,由正弦定理可得:sin(A+B)=2sinBcosA+sinB,
可得:sinAcosB+cosAsinB=2sinBcosA+sinB,
解得:cos2B+sin2B=2sin2B+sinB=1,即:2sin2B+sinB﹣1=0,
可得:sinB= ![]() 或﹣1(舍去).即B=
或﹣1(舍去).即B= ![]() .
.
【解析】(1)由余弦定理化簡已知等式,整理可得:a2=b2+bc,代入已知即可解得c的值.(2)由題意A+B= ![]() ,可得sinA=cosB,cosA=sinB,由正弦定理化簡已知等式可得:2sin2B+sinB﹣1=0,解得sinB,即可求B=
,可得sinA=cosB,cosA=sinB,由正弦定理化簡已知等式可得:2sin2B+sinB﹣1=0,解得sinB,即可求B= ![]() .
.


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:高中數學 來源: 題型:
【題目】如圖(1)所示,已知四邊形![]() 是由直角△
是由直角△![]() 和直角梯形
和直角梯形![]() 拼接而成的,其中
拼接而成的,其中![]()
![]() .且點
.且點![]() 為線段
為線段![]() 的中點,
的中點, ![]() ,
, ![]() 現將△
現將△![]() 沿
沿![]() 進行翻折,使得二面角
進行翻折,使得二面角![]()
![]() 的大小為
的大小為![]() ,得到圖形如圖(2)所示,連接
,得到圖形如圖(2)所示,連接![]() ,點
,點![]() 分別在線段
分別在線段![]() 上.
上.


(1)證明: ![]() ;
;
(2)若三棱錐![]() 的體積為四棱錐
的體積為四棱錐![]() 體積的
體積的![]() ,求點
,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦點在
的焦點在![]() 軸上,且橢圓
軸上,且橢圓![]() 的焦距為2.
的焦距為2.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,過
,過![]() 作
作![]() 軸且與橢圓
軸且與橢圓![]() 交于另一點
交于另一點![]() ,
, ![]() 為橢圓
為橢圓![]() 的右焦點,求證:三點
的右焦點,求證:三點![]() 在同一條直線上.
在同一條直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】完成下列進位制之間的轉化.
(1)10231(4)=________(10);
(2)235(7)=________(10);
(3)137(10)=________(6);
(4)1231(5)=________(7);
(5)213(4)=________(3);
(6)1010111(2)=________(4).
查看答案和解析>>
科目:高中數學 來源: 題型:
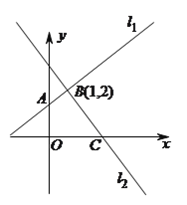
【題目】如圖,經過點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() 和
和![]() ,直線
,直線![]() 交
交![]() 軸正半軸于點
軸正半軸于點![]() ,直線
,直線![]() 交
交![]() 軸正半軸于點
軸正半軸于點![]() .
.
(1)如果![]() ,求點
,求點![]() 的坐標.
的坐標.
(2)試問是否總存在經過![]() ,
, ![]() ,
, ![]() ,
, ![]() 四點的圓?如果存在,求出半徑最小的圓的方程;如果不存在,請說明理由.
四點的圓?如果存在,求出半徑最小的圓的方程;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】濱湖區擬建一主題游戲園,該游戲園為四邊形區域ABCD,其中三角形區城ABC為主題活動區,其中∠ACB=60°,∠ABC=45°,AB=12 ![]() m;AD、CD為游客通道(不考慮寬度),且∠ADC=120°,通道AD、CD圍成三角形區域ADC為游客休閑中心,供游客休憩.
m;AD、CD為游客通道(不考慮寬度),且∠ADC=120°,通道AD、CD圍成三角形區域ADC為游客休閑中心,供游客休憩. 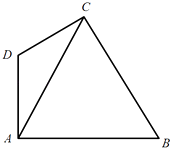
(1)求AC的長度;
(2)記游客通道AD與CD的長度和為L,求L的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某年級舉辦團知識競賽.![]() 、
、![]() 、
、![]() 、
、![]() 四個班報名人數如下:
四個班報名人數如下:
班別 |
|
|
|
|
人數 | 45 | 60 | 30 | 15 |
年級在報名的同學中按分層抽樣的方式抽取10名同學參加競賽,每位參加競賽的同學從10個關于團知識的題目中隨機抽取4個作答,全部答對的同學獲得一份獎品.
(Ⅰ)求各班參加競賽的人數;
(Ⅱ)若![]() 班每位參加競賽的同學對每個題目答對的概率均為
班每位參加競賽的同學對每個題目答對的概率均為![]() ,求
,求![]() 班恰好有2位同學獲得獎品的概率;
班恰好有2位同學獲得獎品的概率;
(Ⅲ)若這10個題目,小張同學只有2個答不對,記小張答對的題目數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是首項為a1= ![]() ,公比q=
,公比q= ![]() 的等比數列,設bn+2=3
的等比數列,設bn+2=3 ![]() an(n∈N*),數列{cn}滿足cn=anbn .
an(n∈N*),數列{cn}滿足cn=anbn .
(1)求證:{bn}是等差數列;
(2)求數列{cn}的前n項和Sn;
(3)若cn≤ ![]() +m﹣1對一切正整數n恒成立,求實數m的取值范圍.
+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com