【題目】若函數(shù)
滿足（1）對于定義域上的任意
，恒有
；（2）對于定義域上的任意
當
時，恒有
，則稱函數(shù)為“理想函數(shù)”，給出下列四個函數(shù)中：① 
； ②
；③
；④
，則被稱為“理想函數(shù)”的有（ ）
A.①B.②④C.③D.④
【答案】B
【解析】
先理解“理想函數(shù)”的定義，再考查各函數(shù)的奇偶性及單調性，對于分段函數(shù)，畫出函數(shù)圖像，再觀察圖像即可得解.
解：由題意可得“理想函數(shù)”為奇函數(shù)且在定義域上為減函數(shù)，
對于①，
的定義域為
，函數(shù)
的減區(qū)間為
，即函數(shù)在上不為減函數(shù)，即①不為“理想函數(shù)”；
對于②，
為
上的減函數(shù)且為奇函數(shù)，即②為“理想函數(shù)”；
對于③，
，即函數(shù)
不為奇函數(shù)，即③不為“理想函數(shù)”；
對于④，函數(shù)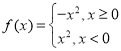
的圖像如圖所示，由圖可知④為“理想函數(shù)”；
即被稱為“理想函數(shù)”的有②④，
故選：B.
科目：高中數(shù)學 來源： 題型：
【題目】2019年4月23日“世界讀書日”來臨之際，某校為了了解中學生課外閱讀情況，隨機抽取了100名學生，并獲得了他們一周課外閱讀時間（單位：小時）的數(shù)據(jù)，按閱讀時間分組：第一組[0,5), 第二組[5,10)，第三組[10,15)，第四組[15,20)，第五組[20,25]，繪制了頻率分布直方圖如下圖所示。已知第三組的頻數(shù)是第五組頻數(shù)的3倍。
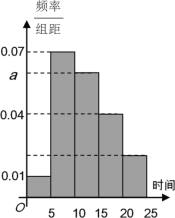
（1）求
的值，并根據(jù)頻率分布直方圖估計該校學生一周課外閱讀時間的平均值；
（2）現(xiàn)從第三、四、五這3組中用分層抽樣的方法抽取6人參加校“中華詩詞比賽”。經(jīng)過比賽后，從這6人中隨機挑選2人組成該校代表隊，求這2人來自不同組別的概率。
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】函數(shù)f(x)的定義域為(0，＋∞)，且對一切x>0，y>0都有
，當
時，有
(1)求f(1)的值；
(2)判斷f(x)的單調性并加以證明；
(3)若f(4)＝2，求f(x)在[1,16]上的值域．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】氣象意義上，從春季進入夏季的標志為：“連續(xù)5天的日平均溫度不低于22℃”.現(xiàn)有甲、乙、丙三地連續(xù)5天的日平均溫度的記錄數(shù)據(jù)（記錄數(shù)據(jù)都是正整數(shù)）：
①甲地：5個數(shù)據(jù)的中位數(shù)為24，眾數(shù)為22；
②乙地：5個數(shù)據(jù)的中位數(shù)為27，總體均值為24；
③丙地：5個數(shù)據(jù)的中有一個數(shù)據(jù)是32，總體均值為26，總體方差為10.8；
則肯定進入夏季的地區(qū)的有（ ）
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
是定義R的奇函數(shù)，當
時，
.
（1）求函數(shù) 的解析式；
（2）畫出函數(shù)的簡圖(不需要作圖步驟)，并求其單調遞增區(qū)間
（3）當
時，求關于m的不等式
的解集．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在
中，角
， 
， 
所對的邊分別為
， 
， 
，且
.
（Ⅰ）求角
的大小；
（Ⅱ）已知
， 
的面積為
，求
的周長.
【答案】（Ⅰ）
.（Ⅱ）
.
【解析】【試題分析】(I)利用正弦定理和三角形內角和定理化簡已知,可求得
的值,進而求得
的大小.(II)利用余弦定理和三角形的面積公式列方程組求解的
的值,進而求得三角形周長.
【試題解析】
（Ⅰ）由
及正弦定理得， 
，
，∴
，
又∵
，∴
.
又∵
，∴
.
（Ⅱ）由
， 
，根據(jù)余弦定理得
，
由
的面積為
，得
.
所以
，得
，
所以
周長
.
【題型】解答題
【結束】
18
【題目】為促進農業(yè)發(fā)展，加快農村建設，某地政府扶持興建了一批“超級蔬菜大棚”.為了解大棚的面積與年利潤之間的關系，隨機抽取了其中的7個大棚，并對當年的利潤進行統(tǒng)計整理后得到了如下數(shù)據(jù)對比表：
大棚面積（畝） | 4.5 | 5.0 | 5.5 | 6.0 | 6.5 | 7.0 | 7.5 |
年利潤（萬元） | 6 | 7 | 7.4 | 8.1 | 8.9 | 9.6 | 11.1 |
由所給數(shù)據(jù)的散點圖可以看出，各樣本點都分布在一條直線附近，并且
與
有很強的線性相關關系.
（Ⅰ）求
關于
的線性回歸方程；
（Ⅱ）小明家的“超級蔬菜大棚”面積為8.0畝，估計小明家的大棚當年的利潤為多少；
（Ⅲ）另外調查了近5年的不同蔬菜畝平均利潤（單位：萬元），其中無絲豆為：1.5，1.7，2.1，2.2，2.5；彩椒為：1.8，1.9，1.9，2.2，2.2，請分析種植哪種蔬菜比較好？
參考數(shù)據(jù)： 
， 
.
參考公式： 
， 
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在用二分法求方程
在區(qū)間
內的近似解時，先將方程變形為
，構建
，然后通過計算以判斷
及
的正負號，再按步驟取區(qū)間中點值，計算中點的函數(shù)近似值，如此往復縮小零點所在區(qū)間，計算得部分數(shù)據(jù)列表如下：
步驟 | 區(qū)間左端點 | 區(qū)間右端點 |
| 中點 |
1 | 2 | 3 | 2.5 | -0.102 |
2 | 0.189 | |||
3 | 2.625 | 0.044 | ||
4 | 2.5 | 2.625 | 2.5625 | -0.029 |
5 | 2.5625 | 2.625 | 2.59375 | 0.008 |
6 | 2.5625 | 2.59375 | 2.578125 | -0.011 |
7 | 2.578125 | 2.59375 | 2.5859375 | -0.001 |
8 | 2.5859375 | 2.59375 | 2.58984375 | 0.003 |
9 | 2.5859375 | 2.58984375 | 2.587890625 | 0.001 |
（1）判斷及的正負號；
（2）請完成上述表格，在空白處填上正確的數(shù)字；
（3）若給定的精確度為0.1，則到第幾步驟即可求出近似值？此時近似值為多少？
（4）若給定的精確度為0.01，則需要到第幾步驟才可求出近似值？近似值為多少？
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
