
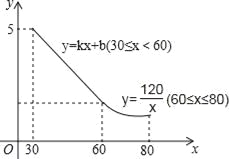
【題目】某工藝品廠生產一種汽車裝飾品,每件生產成本為20元,銷售價格在30元至80元之間(含30元和80元),銷售過程中的管理、倉儲、運輸等各種費用(不含生產成本)總計50萬元,其銷售量y(萬個)與銷售價格(元/個)的函數關系如圖所示.
(1)當30≤x≤60時,求y與x的函數關系式;
(2)求出該廠生產銷售這種產品的純利潤w(萬元)與銷售價格x(元/個)的函數關系式;
(3)銷售價格應定為多少元時,獲得利潤最大,最大利潤是多少?
【答案】(1)y=﹣0.1x+8(30≤x≤60)(2)w=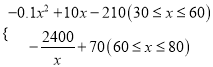 (3)當銷售價格定為50元/件或80元/件,獲得利潤最大,最大利潤是40萬元
(3)當銷售價格定為50元/件或80元/件,獲得利潤最大,最大利潤是40萬元
【解析】試題分析:(1)由圖象知,當30≤x≤60時,圖象過(60,2)和(30,5),運用待定系數法求解析式即可;
(2)根據銷售產品的純利潤=銷售量×單個利潤,分30≤x≤60和60<x≤80列函數表達式;
(3)當30≤x≤60時,運用二次函數性質解決,當60<x≤80時,運用反比例函數性質解答.
試題解析:(1)當x=60時,y=![]() =2,
=2,
∴當30≤x≤60時,圖象過(60,2)和(30,5),
設y=kx+b,則![]() ,
,
解得: ![]() ,
,
∴y=﹣0.1x+8(30≤x≤60);
(2)根據題意,當30≤x≤60時,W=(x﹣20)y﹣50=(x﹣20)(﹣0.1x+8)﹣50=![]() +10x﹣210,
+10x﹣210,
當60<x≤80時,W=(x﹣20)y﹣50=(x﹣20)![]() ﹣50=
﹣50=![]() +70,
+70,
綜上所述:W=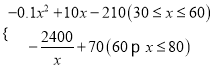 ;
;
(3)當30≤x≤60時,W=![]() +10x﹣210=
+10x﹣210=![]() ,
,
當x=50時, ![]() =40(萬元);
=40(萬元);
當60<x≤80時,W=![]() +70,
+70,
∵﹣2400<0,W隨x的增大而增大,
∴當x=80時, ![]() =
=![]() +70=40(萬元),
+70=40(萬元),
答:當銷售價格定為50元/件或80元/件,獲得利潤最大,最大利潤是40萬元.


科目:初中數學 來源: 題型:
【題目】某班的一次數學小測驗中,共出了20道數學選擇題,做對一題得5分,做錯一題扣1分,小明得分82分,他一共做對了______道題.( )
A. 19 B. 18 C. 17 D. 16
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為調查本校學生平均每天完成作業所用時間的情況,隨機調查了50名同學,如圖是根據調查所得數據繪制的統計圖的一部分.
請根據以上信息,解答下列問題:
(1)將統計圖補充完整;
(2)若該校共有1 800名學生,根據以上調查結果估計該校全體學生平均每天完成作業所用總時間.

查看答案和解析>>
科目:初中數學 來源: 題型:
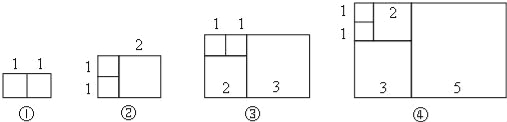
【題目】如圖,將邊長分別為1、2、3、5、…的若干正方形按一定的規律拼成不同的矩形,依次記作矩形①、矩形②、矩形③、矩形④,那么按此規律.
(1)組成第n個矩形的正方形的個數為 個;
(2)求矩形⑥的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,把一張長方形卡片ABCD放在每格寬度為12mm的橫格紙中,恰好四個頂點都在橫格線上,已知∠α=36°,求長方形卡片的周長.(精確到1mm)(參考數據:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
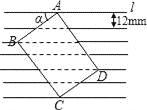
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2016年G20峰會將于9月4﹣5日在杭州舉行,“絲綢細節”助力杭州打動世界,某絲綢公司為G20設計手工禮品.投入W元錢,若以2條領帶和1條絲巾為一份禮品,則剛好可制作600份禮品;若以1條領帶和3條絲巾為一份禮品,則剛好可制作400份獎品.
(1)若W=24萬元,求領帶及絲巾的制作成本各是多少?
(2)若用W元錢全部用于制作領帶,總共可以制作幾條?
(3)若用W元錢恰好能制作300份其他的禮品,可以選擇a條領帶和b條絲巾作為一份禮品(兩種都要有),請求出所有可能的a、b值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com