
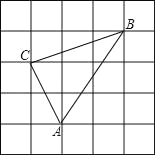
【題目】如圖,方格紙中小正方形的邊長為1,△ABC的三個頂點都在小正方形的格點上,求:
(1)邊AC,AB,BC的長;
(2)點C到AB邊的距離;
(3)求△ABC的面積.
 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:初中數學 來源: 題型:
【題目】旋轉變換是解決數學問題中一種重要的思想方法,通過旋轉變換可以將分散的條件集中到一起,從而方便解決問題.已知,![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 在邊
在邊![]() 上,且
上,且![]() .
.

(1)如圖![]() ,當
,當![]() 時,將
時,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 到
到![]() 的位置,連接
的位置,連接![]() ,
,
①求![]() 的度數;
的度數;
②求證:![]() ;
;
(2)如圖![]() ,當
,當![]() 時,猜想
時,猜想![]() 、
、![]() 、
、![]() 的數量關系,并說明理由;
的數量關系,并說明理由;
(3)如圖![]() ,當
,當![]() ,
,![]() ,
,![]() 時,請直接寫出
時,請直接寫出![]() 的長為________.
的長為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正△ABC中,D,E分別在AC,AB上,且 ![]() ,AE=BE,則有( )
,AE=BE,則有( )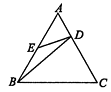
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數 ![]() 的圖象經過坐標原點,與x軸的另一個交點為A(-2,0).
的圖象經過坐標原點,與x軸的另一個交點為A(-2,0).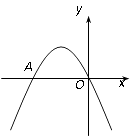
(1)求二次函數的解析式
(2)在拋物線上是否存在一點P,使△AOP的面積為3,若存在請求出點P的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,解決下列問題:
材料一:對非負實數x“四舍五入”到個位的值記為![]() ,即:當n為非負整數時,如果
,即:當n為非負整數時,如果![]() ,則
,則![]() ;反之,當n為非負整數時,如果
;反之,當n為非負整數時,如果![]() ;則
;則![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]()
材料二:平面直角坐標系中任意兩點![]() ,
,![]() ,我們把
,我們把![]() 叫做
叫做![]() 、
、![]() 兩點間的折線距離,并規定
兩點間的折線距離,并規定![]() 若
若![]() 是一定點,
是一定點,![]() 是直線
是直線![]() 上的一動點,我們把
上的一動點,我們把![]() 的最小值叫做
的最小值叫做![]() 到直線
到直線![]() 的折線距離,例如:若
的折線距離,例如:若![]() ,
,![]() 則
則![]() .
.
![]() 如果
如果![]() ,寫出實數x的取值范圍;
,寫出實數x的取值范圍;![]() 已知點
已知點![]() ,點
,點![]() ,且
,且![]() ,求a的值.
,求a的值.
![]() 若m為滿足
若m為滿足![]() 的最大值,求點
的最大值,求點![]() 到直線
到直線![]() 的折線距離.
的折線距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=1,點D、E在直線BC上運動,設BD=x,CE=y.如果∠BAC=30°,∠DAE=105°,則y與x之間的函數關系式為.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初三年級的一場籃球比賽中,如圖隊員甲正在投籃,已知球出手時離地面高 ![]() m,與籃圈中心的水平距離為7m,當球出手后水平距離為4m時到達最大高度4m,設籃球運行的軌跡為拋物線,籃圈距地面3m.
m,與籃圈中心的水平距離為7m,當球出手后水平距離為4m時到達最大高度4m,設籃球運行的軌跡為拋物線,籃圈距地面3m.
(1)建立如圖所示的平面直角坐標系,求拋物線的解析式并判斷此球能否準確投中?
(2)此時,若對方隊員乙在甲前面1m處跳起蓋帽攔截,已知乙的最大摸高為3.1m,那么他能否獲得成功?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的函數圖象與x軸、y軸分別交于點A、B,以線段AB為直角邊在第一象限內作Rt△ABC,且使∠ABC=30°.
的函數圖象與x軸、y軸分別交于點A、B,以線段AB為直角邊在第一象限內作Rt△ABC,且使∠ABC=30°.
(1)求△ABC的面積;
(2)如果在第二象限內有一點P(m,![]() ),試用含m的代數式表示△APB的面積,并求當△APB與△ABC面積相等時m的值;
),試用含m的代數式表示△APB的面積,并求當△APB與△ABC面積相等時m的值;
(3)是否存在使△QAB是等腰三角形并且在坐標軸上的點Q?若存在,請寫出點Q所有可能的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在Rt△ABC中,∠ACB=90°,D、E分別是AB、AC的中點,F是BC延長線上的一點,且EF∥DC.(1)求證:四邊形CDEF是平行四邊形;(2)若EF=2cm,求AB的長.
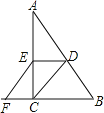
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com