
【題目】計算:
(1)計算:(﹣1)3÷(﹣5)2×(﹣![]() )﹣|0.8﹣1|;
)﹣|0.8﹣1|;
(2)計算:(1![]() +
+![]() ﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
(3)先化簡,再求值,已知|x+2|+(y﹣![]() )2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
)2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
【答案】(1)![]() ;(2)28;(3)8.
;(2)28;(3)8.
【解析】
(1)先計算乘方,絕對值,再計算乘除,最后加減得結果;(2)先計算乘方和絕對值,再運用乘法對加法的分配律,最后加減得結果;(3)利用非負數的性質,先確定x、y的值,再化簡整式,最后代入求值.
(1)原式=﹣1÷25×(﹣![]() )﹣0.2
)﹣0.2
=1×![]() ×
×![]() ﹣
﹣![]()
=![]() ﹣
﹣![]()
=﹣![]() ;
;
(2)原式=(![]() +
+![]() ﹣
﹣![]() )×(﹣24)﹣1﹣2
)×(﹣24)﹣1﹣2
=﹣32﹣3+66﹣1﹣2
=28;
(3)∵|x+2|+(y﹣![]() )2=0,
)2=0,
又∵|x+2|≥0,(y﹣![]() )2≥0,
)2≥0,
∴x+2=0,y﹣![]() =0,
=0,
∴x=﹣2,y=![]() .
.
3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]
=3x2﹣6xy﹣(3x2﹣2y+2xy+2y)
=3x2﹣6xy﹣3x2+2y﹣2xy﹣2y
=﹣8xy.
當x=﹣2,y=![]() 時,
時,
原式=﹣8×(﹣2)×![]()
=8.


科目:初中數學 來源: 題型:
【題目】課間休息時小明拿著兩根木棒玩,小華看到后要小明給他玩,小明說:“較短木棒AB長40cm,較長木棒CD長60cm,將它們的一端重合,放在同一條直線上,此時兩根木棒的中點分別是點E和點F,則點E和點F間的距離是多少?你說對了我就給你玩”聰明的你請幫小華求出此時兩根木棒的中點E和F間的距離是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖A在數軸上所對應的數為﹣2.
(1)點B在點A右邊距A點4個單位長度,求點B所對應的數;
(2)在(1)的條件下,點A以每秒2個單位長度沿數軸向左運動,點 B 以每秒2個單位長度沿數軸向右運動,當點A運動到﹣6所在的點處時,求A,B兩點間距離.
(3)在(2)的條件下,現A點靜止不動,B點再以每秒2個單位長度沿數軸向左運動時,經過多長時間A,B兩點相距4個單位長度.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E在以AB為直徑的⊙O上,點C是 ![]() 的中點,過點C作CD垂直于AE,交AE的延長線于點D,連接BE交AC于點F.
的中點,過點C作CD垂直于AE,交AE的延長線于點D,連接BE交AC于點F. 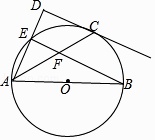
(1)求證:CD是⊙O的切線;
(2)若cos∠CAD= ![]() ,BF=15,求AC的長.
,BF=15,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y1=x+1與雙曲線![]() (k>0)相交于點A、B,已知點A坐標(2,m).
(k>0)相交于點A、B,已知點A坐標(2,m).
(1)求k的值;
(2)求點B的坐標,并觀察圖象,寫出當![]() 時,x的取值范圍.
時,x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,將一點(橫坐標與縱坐標不相等)的橫坐標與縱坐標互換后得到的點叫這一點的“互換點”,如(﹣3,5)與(5,﹣3)是一對“互換點”.
(1)任意一對“互換點”能否都在一個反比例函數的圖象上?為什么?
(2)M、N是一對“互換點”,若點M的坐標為(m,n),求直線MN的表達式(用含m、n的代數式表示);
(3)在拋物線y=x2+bx+c的圖象上有一對“互換點”A、B,其中點A在反比例函數y=﹣ ![]() 的圖象上,直線AB經過點P(
的圖象上,直線AB經過點P( ![]() ,
, ![]() ),求此拋物線的表達式.
),求此拋物線的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知凸五邊形ABCDE的邊長均相等,且∠DBE=∠ABE+∠CBD,AC=1,則BD必定滿足( ) 
A.BD<2
B.BD=2
C.BD>2
D.以上情況均有可能
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com