
【題目】如圖,將矩形ABCD繞點C沿順時針方向旋轉90°到矩形A′B′CD′的位置,AB=2,AD=4,則陰影部分的面積為 . 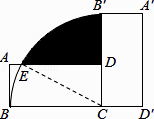
【答案】![]() π﹣2
π﹣2 ![]()
【解析】解:∵四邊形ABCD是矩形, ∴AD=BC=4,CD=AB=2,∠BCD=∠ADC=90°,
∴CE=BC=4,
∴CE=2CD,
∴∠DEC=30°,
∴∠DCE=60°,
由勾股定理得:DE=2 ![]() ,
,
∴陰影部分的面積是S=S扇形CEB′﹣S△CDE= ![]() ﹣
﹣ ![]() ×2×2
×2×2 ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考點精析】利用扇形面積計算公式和旋轉的性質對題目進行判斷即可得到答案,需要熟知在圓上,由兩條半徑和一段弧圍成的圖形叫做扇形;扇形面積S=π(R2-r2);①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了.


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的對角線AC=3cm,把它沿對角線AC方向平移1cm得到菱形EFGH,則圖中陰影部分圖形的面積與四邊形ENCM的面積之比為( ) 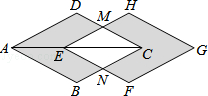
A.9:4
B.12:5
C.3:1
D.5:2
查看答案和解析>>
科目:初中數學 來源: 題型:
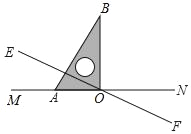
【題目】如圖,直線EF與MN相交于點O,∠MOE=30°,將一直角三角尺的直角頂點與點O重合,直角邊OA與MN重合,OB在∠NOE內部.操作:將三角尺繞點O以每秒5°的速度沿順時針方向旋轉一周,設運動時間為t(s).
(1)當t為何值時,直角邊OB恰好平分∠NOE?此時OA是否平分∠MOE?請說明理由;
(2)若在三角尺轉動的同時,直線EF也繞點O以每秒8°的速度順時針方向旋轉一周,當一方先完成旋轉一周時,另一方同時停止轉動.
①當t為何值時,OE平分∠AOB?
②OE能否平分∠NOB?若能請直接寫出t的值;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】歷史上的數學巨人歐拉最先把關于x的多項式用記號f(x)來表示,例如f(x)=x2+3x﹣5,把x=某數時多項式的值用f(某數)來表示,例如x=1時多項式x2+3x﹣5的值記為f(1)=12+3×1﹣5=﹣1.
(1)已知g(x)=﹣2x2﹣3x+1,分別求出g(﹣1)和g(﹣2)的值.
(2)已知h(x)=ax3+2x2﹣x﹣14,![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,E,F分別是BC,AC的中點,以AC為斜邊作Rt△ADC,若∠CAD=∠CAB=45°,則下列結論不正確的是( ) 
A.∠ECD=112.5°
B.DE平分∠FDC
C.∠DEC=30°
D.AB= ![]() CD
CD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,![]() ,
,![]() 的平分線與BC的延長線交于點E,與DC交于點F,且點F為邊DC的中點,
的平分線與BC的延長線交于點E,與DC交于點F,且點F為邊DC的中點,![]() ,垂足為G,若
,垂足為G,若![]() ,則AE的邊長為
,則AE的邊長為![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有四張背面完全相同的紙牌A、B、C、D,其正面分別畫有四個不同的幾何圖形,將這四張紙牌背面朝上洗勻.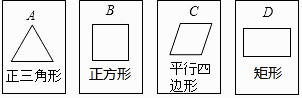
(1)從中隨機摸出一張,求摸出的牌面圖形是中心對稱圖形的概率;
(2)小明和小亮約定做一個游戲,其規則為:先由小明隨機摸出一張紙牌,不放回,再由小亮從剩下的紙牌中隨機摸出一張,若摸出的兩張牌面圖形都是軸對稱圖形小明獲勝,否則小亮獲勝,這個游戲公平嗎?請用列表法(或樹狀圖)說明理由(紙牌用A、B、C、D表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)計算:(﹣1)3÷(﹣5)2×(﹣![]() )﹣|0.8﹣1|;
)﹣|0.8﹣1|;
(2)計算:(1![]() +
+![]() ﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
﹣2.75)×(﹣24)+(﹣1)2011﹣|﹣2|;
(3)先化簡,再求值,已知|x+2|+(y﹣![]() )2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
)2=0,求3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)]的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 的解析表達式為:y=-3x+3,且
的解析表達式為:y=-3x+3,且![]() 與x軸交于點D,直線
與x軸交于點D,直線![]() 經過點A,B,直線
經過點A,B,直線![]() ,
,![]() 交于點C.
交于點C.
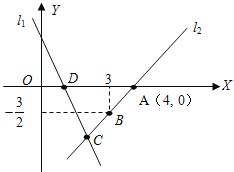
(1)求點D的坐標;
(2)求直線![]() 的解析表達式;
的解析表達式;
(3)求△ADC的面積;
(4)在直線![]() 上存在異于點C的另一點P,使得△ADP的面積是△ADC面積的2倍,請直接寫出點P的坐標.
上存在異于點C的另一點P,使得△ADP的面積是△ADC面積的2倍,請直接寫出點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com