
【題目】實驗證明,平面鏡反射光線的規(guī)律是:照射到平面鏡上的光線和被反射出的光線與平面鏡所夾的銳角相等.
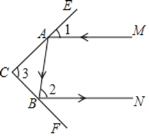
如圖,一束光線MA照射到平面鏡CE上,被CE反射到平面鏡CF上,又被CF反射.已知被CF反射出的光線BN與光線MA平行.若∠1=35°,則∠2= ,∠3= ;若∠1=50°,∠3= .
(2)由(1)猜想:當兩平面鏡CE,CF的夾角∠3為多少度時,可以使任何射到平面鏡CE上的光線MA,經過平面鏡CE,CF的兩次反射后,入射光線MA與反射光線BN平行,請你寫出推理過程.
【答案】(1)70°,90°,90°;(2)猜想:當兩平面鏡CE,CF的夾角∠3為90°時,可以使任何射到平面鏡CE上的光線MA,經過平面鏡CE,CF的兩次反射后,入射光線MA與反射光線BN平行.理由見解析.
【解析】
(1)根據平行線的性質和三角形內角和,以及入射角等于反射角,可以求得∠2和∠3的度數(shù);
(2)先寫出∠3等于多少度,然后根據題意和圖形結合第(1)問的提示思路,即可寫出推理過程.
解:(1)∵AM∥BN,
∴∠MAB+∠2=180°,
∵∠MAB+∠1+∠BAC=180°,∠1=∠BAC,∠1=35°,
∴∠2=2∠1=70°,
∵∠2+∠ABC+∠NBF=180°,∠ABC=∠NBF,
∴∠ABC=55°,
∴∠3=180°-∠BAC-∠ABC=90°;
當∠1=50°時, 同理可得,∠2=100°,∠ABC=40°,∠BAC=∠1=50°,
則∠3=180°-∠BAC-∠ABC=90°;
故答案為:70°,90°,90°;
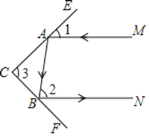
(2)猜想:當兩平面鏡CE,CF的夾角∠3為90°時,可以使任何射到平面鏡CE上的光線MA,經過平面鏡CE,CF的兩次反射后,入射光線MA與反射光線BN平行.
理由:∵∠3=90°,
∴∠BAC+∠ABC=90°,
∵∠1=∠BAC,∠ABC=∠NBF,
∴∠BAC+∠1+∠ABC+∠NBF=180°,
∴∠MAB+∠2=180°,
∴MA∥BN.


科目:初中數(shù)學 來源: 題型:
【題目】一袋中裝有形狀大小都相同的四個小球,每個小球上各標有一個數(shù)字,分別是1,4,7,8.現(xiàn)規(guī)定從袋中任取一個小球,對應的數(shù)字作為一個兩位數(shù)的個位數(shù);然后將小球放回袋中并攪拌均勻,再任取一個小球,對應的數(shù)字作為這個兩位數(shù)的十位數(shù).
(1)寫出按上述規(guī)定得到所有可能的兩位數(shù);
(2)從這些兩位數(shù)中任取一個,求其算術平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】甲有存款600元,乙有存款2000元,從本月開始,他們進行零存整取儲蓄,甲每月存款500元,乙每月存款200元.
(1)列出甲、乙的存款額y1、y2(元)與存款月數(shù)x(月)之間的函數(shù)關系式,畫出函數(shù)圖象.
(2)請問到第幾個月,甲的存款額超過乙的存款額?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某商店第一次用300元購進筆記本若干,第二次又用300元購進該款筆記本,但這次每本的進價是第一次進價的 ![]() 倍,購進數(shù)量比第一次少了25本.
倍,購進數(shù)量比第一次少了25本.
(1)求第一次每本筆記本的進價是多少元?
(2)若要求這兩次購進的筆記本按同一價格全部銷售完畢后獲利不低于450元,問每本筆記本的售價至少是多少元?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】若x滿足(x-4) (x-9)=6,求(x-4)2+(x-9)2的值.
解:設x-4=a,x-9=b,則(x-4)(x-9)=ab=6,a-b=(x-4)-(x-9)=5,
∴(x-4)2+(x-9)2=a2+b2=(a-b)2+2ab=52+2×6=37
請仿照上面的方法求解下面問題:
(1)若x滿足(x-2)(x-5)=10,求(x-2)2 + (x-5)2的值
(2)已知正方形ABCD的邊長為x,E,F分別是AD、DC上的點,且AE=1,CF=3,長方形EMFD的面積是15,分別以MF、DF作正方形,求陰影部分的面積.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知分式A=![]() .
.
(1) 化簡這個分式;
(2) 當a>2時,把分式A化簡結果的分子與分母同時加上3后得到分式B,問:分式B的值較原來分式A的值是變大了還是變小了?試說明理由.
(3) 若A的值是整數(shù),且a也為整數(shù),求出符合條件的所有a值的和.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖1所示,一次函數(shù)y=kx+b的圖象與反比例函數(shù)![]() 的圖象交于
的圖象交于![]() ,
, ![]() 兩點.
兩點.
(1)求一次函數(shù)和反比例函數(shù)的解析式;
(2)設點![]() 和
和![]() 是反比例函數(shù)
是反比例函數(shù)![]() 圖象上兩點,若
圖象上兩點,若![]() ,求
,求![]() 的值;
的值;
(3)若M(x1,y1)和N(x2,y2)兩點在直線AB上,如圖2所示,過M、N兩點分別作y軸的平行線交雙曲線于E、F,已知﹣3<x1<0,x2>1,請?zhí)骄慨?/span>x1、x2滿足什么關系時,MN∥EF.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
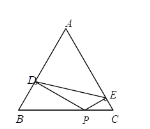
【題目】如圖,△ABC 是等邊三角形,P 是 BC 上任意一點,PD⊥AB,PE⊥AC,連接 DE.記△ADE 的周長為![]() ,四邊形 BDEC 的周長為
,四邊形 BDEC 的周長為![]() ,則
,則![]() 與
與![]() 的大小關系是( )
的大小關系是( )
A. ![]() =
=![]() B.
B. ![]() >
>![]() C.
C. ![]() <
<![]() D. 無法確定
D. 無法確定
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某移動通信公司推出了如下兩種移動電話計費方式,
月使用費/元 | 主叫限定時間/分鐘 | 主叫超時費(元/分鐘) | |
方式一 | 30 | 600 | 0.20 |
方式二 | 50 | 600 | 0.25 |
說明:月使用費固定收取,主叫不超過限定時間不再收費,超過部分加收超時費.例如,方式一每月固定交費30元,當主叫計時不超過300分鐘不再額外收費,超過300分鐘時,超過部分每分鐘加收0.20元(不足1分鐘按1分鐘計算)
(1)請根據題意完成如表的填空;
月主叫時間500分鐘 | 月主叫時間800分鐘 | |
方式一收費/元 |
| 130 |
方式二收費/元 | 50 |
|
(2)設某月主叫時間為t(分鐘),方式一、方式二兩種計費方式的費用分別為y1(元),y2(元),分別寫出兩種計費方式中主叫時間t(分鐘)與費用為y1(元),y2(元)的函數(shù)關系式;
(3)請計算說明選擇哪種計費方式更省錢.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com