
【題目】在平面直角坐標系中,已知直線y=﹣![]() x+3與x軸、y軸分別交于A、B兩點,點C在線段OB上,把△ABC沿直線AC折疊,使點B剛好落在x軸上,則點C的坐標是( )
x+3與x軸、y軸分別交于A、B兩點,點C在線段OB上,把△ABC沿直線AC折疊,使點B剛好落在x軸上,則點C的坐標是( )
A.(0,﹣![]() )B.(0,
)B.(0,![]() )C.(0,3)D.(0,4)
)C.(0,3)D.(0,4)
【答案】B
【解析】
設C(0,n),過C作CD⊥AB于D,先求出A,B的坐標,分別為(4,0),(0,3),得到AB的長,再根據折疊的性質得到AC平分∠OAB,得到CD=CO=n,DA=OA=4,則DB=5﹣4=1,BC=3﹣n,在Rt△BCD中,利用勾股定理得到n的方程,解方程求出n即可.
解:設C(0,n),過C作CD⊥AB于D,如圖,
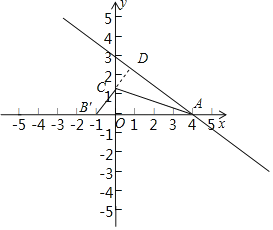
對于直線y=﹣![]() x+3,
x+3,
當x=0,得y=3;
當y=0,x=4,
∴A(4,0),B(0,3),即OA=4,OB=3,
∴AB=5,
又∵坐標平面沿直線AC折疊,使點B剛好落在x軸上,
∴AC平分∠OAB,
∴CD=CO=n,則BC=3﹣n,
∴DA=OA=4,
∴DB=5﹣4=1,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+12=(3﹣n)2,解得n=![]() ,
,
∴點C的坐標為(0,![]() ).
).
故選:B.


 輕松課堂單元測試AB卷系列答案
輕松課堂單元測試AB卷系列答案 小題狂做系列答案
小題狂做系列答案科目:初中數學 來源: 題型:
【題目】端午節是我國的傳統節日,人們素有吃粽子的習俗,某商場在端午節來臨之際用3000元購進![]() 、
、![]() 兩種粽子1100個,購買
兩種粽子1100個,購買![]() 種粽子與購買
種粽子與購買![]() 種粽子的費用相同,已知
種粽子的費用相同,已知![]() 粽子的單價是
粽子的單價是![]() 種粽子單價的1.2倍.
種粽子單價的1.2倍.
(1)求![]() 、
、![]() 兩種粽子的單價各是多少?
兩種粽子的單價各是多少?
(2)若計劃用不超過7000元的資金再次購買![]() 、
、![]() 兩種粽子共2600個,已知
兩種粽子共2600個,已知![]() 、
、![]() 兩種粽子的進價不變,求
兩種粽子的進價不變,求![]() 中粽子最多能購進多少個?
中粽子最多能購進多少個?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四川雅安發生地震后,某校學生會向全校1900名學生發起了“心系雅安”捐款活動,為了解捐款情況,學生會隨機調查了部分學生的捐款金額,并用得到的數據繪制了如下統計圖①和圖②,請根據相關信息,解答下列是問題:
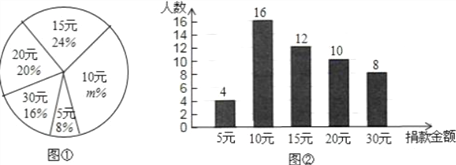
(1)本次接受隨機抽樣調查的學生人數為 ,圖①中m的值是 ;
(2)求本次調查獲取的樣本數據的平均數、眾數和中位數;
(3)根據樣本數據,估計該校本次活動捐款金額為10元的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛貨車從百貨大樓出發負責送貨,向東走了 5 千米到達小明家,繼續向東走了 1.5 千米到達小紅家,然后向西走了 9.5 千米到達小剛家,最后返回百貨大樓.
![]()
(1)以百貨大樓為原點,向東為正方向,1 個單位長度表示 1 千米,請你在數軸上標出小明、小紅、小剛家的位置.(小明家用點 A 表示,小紅家用點 B 表示,小剛家用點 C 表示)
(2)小明家與小剛家相距多遠?
(3)若貨車每千米耗油 0.6 升,那么這輛貨車此次送貨共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“雙劍合璧,天下無敵”,其意思是指兩個人合在一起,取長補短,威力無比.在二次根式中也常有這種相輔相成的“對子”,如:![]() ,
,![]() ,它們的積中不含根號,我們說這兩個二次根式是互為有理化因式,其中一個是另一個的有理化因式,于是,二次根式除法可以這樣解:
,它們的積中不含根號,我們說這兩個二次根式是互為有理化因式,其中一個是另一個的有理化因式,于是,二次根式除法可以這樣解:![]() ,
, .
.
像這樣通過分子、分母同乘一個式子把分母中的根號化去的方法,叫做分母有理化.
解決下列問題:
(1)將![]() 分母有理化得 ;
分母有理化得 ;![]() 的有理化因式是 ;
的有理化因式是 ;
(2)化簡:![]() = ;
= ;
(3)化簡:![]() ……+
……+![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
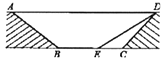
【題目】為緩解交通擁堵,某區擬計劃修建一地下通道,該通道一部分的截面如圖所示(圖中地面![]() 與通道
與通道![]() 平行),通道水平寬度
平行),通道水平寬度![]() 為8米,
為8米, ![]() ,通道斜面
,通道斜面![]() 的長為6米,通道斜面
的長為6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的長為 米;
的長為 米;
(2)為增加市民行走的舒適度,擬將設計圖中的通道斜面![]() 的坡度變緩,修改后的通道斜面
的坡度變緩,修改后的通道斜面![]() 的坡角為30°,求此時
的坡角為30°,求此時![]() 的長.(結果保留根號)
的長.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】冬天來了,曬衣服成了頭疼的事情,聰明的小華想到一個好辦法,在家后院地面(BD)上立兩根等長的立柱AB、CD(均與地面垂直),并在立柱之間懸掛一根繩子.繩子的形狀近似成了拋物線![]() ,如圖1,已知BD=8米,繩子最低點離地面的距離為1米.
,如圖1,已知BD=8米,繩子最低點離地面的距離為1米.
(1)求立柱AB的長度;
(2)由于掛的衣服比較多,為了防止衣服碰到地面,小華用一根垂直于地面的立柱MN撐起繩子(如圖2),MN的長度為1.85米,通過調整MN的位置,使左邊拋物線F1對應函數的二次項系數為![]() ,頂點離地面1.6米,求MN離AB的距離.
,頂點離地面1.6米,求MN離AB的距離.
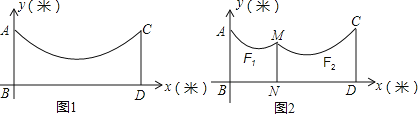
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:小剛站在河邊的![]() 點處,在河的對面(小剛的正北方向)的
點處,在河的對面(小剛的正北方向)的![]() 處有一電線塔,他想知道電線塔離他有多遠,于是他向正西方向走了30步到達一棵樹
處有一電線塔,他想知道電線塔離他有多遠,于是他向正西方向走了30步到達一棵樹![]() 處,接著再向前走了30步到達
處,接著再向前走了30步到達![]() 處,然后他左轉
處,然后他左轉![]() 直行,當小剛看到電線塔、樹與自己現處的位置
直行,當小剛看到電線塔、樹與自己現處的位置![]() 在一條直線時,他共走了140步.
在一條直線時,他共走了140步.

(1)根據題意,畫出示意圖;
(2)如果小剛一步大約50厘米,估計小剛在點![]() 處時他與電線塔的距離,并說明理由.
處時他與電線塔的距離,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在□ABCD中,對角線AC、BD相交于點O,且OA=OB.
(1)求證:四邊形ABCD是矩形;
(2)若AB=6,∠AOB=120°,求BC的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com