
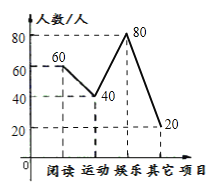
【題目】某校為研究學生的課余活動情況,采取抽樣的方法,從閱讀、運動、娛樂、其它等四個方面調查了若干名學生的興趣愛好,并將調查的結果繪制了如下的兩幅不完整的統計圖(如圖),請你根據圖中提供的信息解答下列問題:


①這次調研,一共調查了 人.
②有閱讀興趣的學生占被調查學生總數的 %.
③有“其它”愛好的學生共多少人?
④補全折線統計圖.
【答案】①200;②30%;③20;④詳見解析
【解析】
①由折線統計圖可以看出愛好運動的人數是40人,由扇形統計圖看出愛好運動的人數占抽樣人數的20%,根據百分數除法的意義,用愛好運動的數除以所占的百分率就是被抽樣調查的人數;
②用有閱讀興趣的學生數(從折線統計圖可以看出)除以被調查總人數(①已求出));
③把被調查的總人數看作單位“1”,用1減去有閱讀興趣、運動興趣、娛樂興趣人數所的百分率就是其它興趣學生人數所占的百分率;根據百分數乘法的意義,用總人數乘其它愛好人數所占的百分率就是有“其它”愛好的學生人數;
④根據百分數乘法的意義,用總人數乘愛好娛樂人數所占的百分率求出愛好娛樂人數,即可補全折線統計圖.
解:①40÷20%= 200 人,
即這次調研,一共調查了200人,
故答案為:200;
②60÷200= 30 %
即有閱讀興趣的學生占被調查學生總數的30%,
故答案為:30%;
③1-20%-40%-30%=10%
200×10%=20(人)
即有“其它”愛好的學生共20人,
故答案為:20;
④200×40%=80(人)
愛好娛樂的80人,“其它”愛好的20人,補全折線統計圖如下:


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:初中數學 來源: 題型:
【題目】方成同學看到一則材料:甲開汽車,乙騎自行車從M地出發沿一條公路勻速前往N地.設乙行駛的時間為t(h),甲乙兩人之間的距離為y(km),y與t的函數關系如圖1所示.
方成思考后發現了如圖1的部分正確信息:乙先出發1h;甲出發0.5小時與乙相遇.
請你幫助方成同學解決以下問題:
(1)分別求出線段BC,CD所在直線的函數表達式;
(2)當20<y<30時,求t的取值范圍;
(3)分別求出甲,乙行駛的路程S甲,S乙與時間t的函數表達式,并在圖2所給的直角坐標系中分別畫出它們的圖象;
(4)丙騎摩托車與乙同時出發,從N地沿同一公路勻速前往M地,若丙經過![]() h與乙相遇,問丙出發后多少時間與甲相遇?
h與乙相遇,問丙出發后多少時間與甲相遇?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AC=3,BC=4,AB=5,D、E分別是邊AB、邊BC上的點,把△ABC沿著直線DE對折,頂點B的對應點是點![]() .
.
(1)如圖1,如果點![]() 和頂點A重合,求CE的長;
和頂點A重合,求CE的長;
(2)如圖2,如果點![]() 落在AC的中點,求CE的長.
落在AC的中點,求CE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在汶川地震十周年紀念日,某教育集團進行了主題捐書活動,同學們熱情高漲,僅僅五天就捐贈圖書m萬冊,其中m與![]() 互為倒數.此時教育集團決定把所捐圖書分批次運往市區周邊的“希望學校”,而捐書活動將再持續一周.下表為活動結束前一周所捐圖書存量的增減變化情況(單位:萬冊):
互為倒數.此時教育集團決定把所捐圖書分批次運往市區周邊的“希望學校”,而捐書活動將再持續一周.下表為活動結束前一周所捐圖書存量的增減變化情況(單位:萬冊):
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 |
+0.2 | +0.1 | ﹣0.1 | ﹣0.4 | +0.3 | +0.5 | ﹣0.1 |
(1)m的值為 .
(2)求活動結束時,該教育集團所捐圖書存量為多少萬冊;
(3)活動結束后,該教育集團決定在6天內把所捐圖書全部運往“希望學校”,現有A、B兩個運輸公司,B運輸公司每天的運輸數量是A運輸公司的1.5倍,學校首先聘請A運輸公司進行運輸,工作兩天后,由于某些原因,A運輸公司每天運輸的數量比原來降低了25%,學校決定又聘請B運輸公司加入,與A運輸公司共同運輸,恰好按時完成任務,求A運輸公司每天運輸多少萬冊圖書?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,∠ACB=90°,點D在BC上,BD=6,DC=2,點P是AB上的動點,則PC+PD的最小值為( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的材料:
如果函數y=f(x)滿足:對于自變量x的取值范圍內的任意x1,x2,
(1)若![]() ,都有
,都有![]() ,則稱f(x)是增函數;
,則稱f(x)是增函數;
(2)若![]() ,都有
,都有![]() ,則稱f(x)是減函數.
,則稱f(x)是減函數.
例題:證明函數f(x)=![]() 是減函數.
是減函數.
證明:設![]() ,
,
![]()
∵![]() ,
,
∴![]() .
.
∴![]() .即
.即![]() .
.
∴![]() .
.
∴函數![]() 是減函數.
是減函數.
根據以上材料,解答下面的問題:
已知函數f(x)=![]() (x<0),例如f(-1)=
(x<0),例如f(-1)=![]() =-3,f(-2)=
=-3,f(-2)=![]() =-
=-![]()
(1)計算:f(-3)= ;
(2)猜想:函數f(x)=![]() (x<0)是 函數(填“增”或“減”);
(x<0)是 函數(填“增”或“減”);
(3)請仿照例題證明你的猜想.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在活動課上,小明和小紅合作用一副三角板來測量學校旗桿高度.已知小明的眼睛與地面的距離(AB)是1.7m,他調整自己的位置,設法使得三角板的一條直角邊保持水平,且斜邊與旗桿頂端M在同一條直線上,測得旗桿頂端M仰角為45°;小紅的眼睛與地面的距離(CD)是1.5m,用同樣的方法測得旗桿頂端M的仰角為30°.兩人相距28米且位于旗桿兩側(點B、N、D在同一條直線上).求出旗桿MN的高度.(參考數據: ![]() ,結果保留整數.)
,結果保留整數.)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用一條長為18cm的細繩圍成一個等腰三角形.
(1)如果腰長是底邊長的2倍,求三角形各邊的長;
(2)能圍成有一邊的長是4cm的等腰三角形嗎?若能,求出其他兩邊的長;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題情景:如圖1,![]() 中,有一塊直角三角板
中,有一塊直角三角板![]() 放置在
放置在![]() 上(
上(![]() 點在
點在![]() 內),使三角板
內),使三角板![]() 的兩條直角邊
的兩條直角邊![]() 、
、![]() 恰好分別經過點
恰好分別經過點![]() 和點
和點![]() .
.
試問![]() 與
與![]() 是否存在某種確定的數量關系?
是否存在某種確定的數量關系?
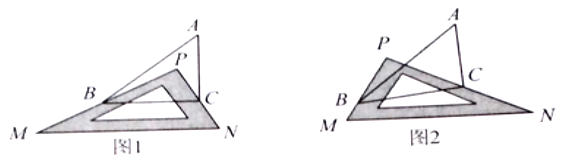
(1)特殊研究:若![]() ,則
,則![]() 度,
度,![]() 度,
度,![]() 度;
度;
(2)類比探索:請探究![]() 與
與![]() 的關系.
的關系.
(3)類比延伸:如圖2,改變直角三角包![]() 的位置;使
的位置;使![]() 點在
點在![]() 外,三角板
外,三角板![]() 的兩條直角邊
的兩條直角邊![]() 、
、![]() 仍然分別經過點
仍然分別經過點![]() 和點
和點![]() ,(2)中的結論是否仍然成立?若不成立請直接寫出你的結論.
,(2)中的結論是否仍然成立?若不成立請直接寫出你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com