
【題目】如圖1,在 ![]() 中,以
中,以 ![]() 為直徑的⊙O,交
為直徑的⊙O,交 ![]() 于點
于點 ![]() ,且
,且 ![]() ,交線段
,交線段 ![]() 的延長線于點
的延長線于點 ![]() ,連接
,連接 ![]() ,過點
,過點 ![]() 作
作 ![]() 于點
于點 ![]() .
.
(Ⅰ)求證: ![]() ;
;
(Ⅱ)在 ![]() 的內部作
的內部作 ![]() ,使
,使 ![]() ,
, ![]() 分別交于
分別交于 ![]() 、
、 ![]() 于點
于點 ![]() 、
、 ![]() ,交⊙O于點
,交⊙O于點 ![]() ,若
,若 ![]() ,求
,求 ![]() 的長.
的長.
【答案】(Ⅰ)證明:過點C作CH⊥BA 交BA的延長線于H,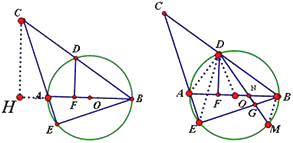
∵ ![]() ,
, ![]() ,
,
∴DF為![]() BHC的中位線,CH=2DF,
BHC的中位線,CH=2DF,
連接AD,
∵AB是直徑,
∴∠ADB=90°,
又∵BD=CD,
∴![]() ABC是等腰三角形∴AB=AC,
ABC是等腰三角形∴AB=AC,
∵∠AEB =90°=∠AHC ,∠BAE =∠CAH
∴![]() AEB≌
AEB≌![]() AHC
AHC
∴CH=BE , ![]()
(Ⅱ)解:連接DA、DO、DE、BM,
∴∠ADE=∠ABE=∠BDM
∵ ![]() , BN=
, BN= ![]() ,
,
∴由(Ⅰ)可知, BE=2DF= ![]() ,
,
∵⊿CEB為直角三角形, BD=CD,
∴DE=DB , 又∠ADE=∠BDN ∠AED=∠DBN
∴![]() ADE≌
ADE≌![]() NDB
NDB
∴AD=DN BN=AE= ![]()
∵AB是直徑,
∴∠ADB=∠AEB =90° BE=2DF= ![]() , AE=
, AE= ![]() . AB=3
. AB=3 ![]()
∵ ![]() AD=DN ∴ FN=AF=
AD=DN ∴ FN=AF= ![]() . DF=
. DF= ![]() ∴DN=3
∴DN=3 ![]()
在![]() ADN與
ADN與![]() BMN中,可證
BMN中,可證![]() ADN∽
ADN∽![]() MBN,得出AN
MBN,得出AN![]() NB=MN
NB=MN![]() DN
DN
∴MN=2 ![]()
在![]() DBG與
DBG與![]() DMB中,
DMB中,
∵DC=DE=DB
∴∠DMB=∠DBE=∠DEB, ∠BDG=∠BDM,
可證![]() DBG∽
DBG∽![]() DMB,
DMB,
得出DB2=DG×DM ![]() ,FB=2
,FB=2 ![]()
∴DB=6, DM=DN+MN=3 ![]() +2
+2 ![]() =5
=5 ![]()
∴36=DG×5 ![]() , DG=
, DG= ![]() ,
,
∴ MG= ![]() .
.
【解析】本題考查全等三角形的判定與性質、相似三角形的判定與性質,注意分析題目中條件,找足![]() AEB和
AEB和![]() AHC全等、
AHC全等、![]() ADE和
ADE和![]() NDB全等,和
NDB全等,和![]() ADN∽
ADN∽![]() MBN、
MBN、![]() DBG∽
DBG∽![]() DMB的條件,推導求解.
DMB的條件,推導求解.
【考點精析】掌握三角形中位線定理和相似三角形的判定與性質是解答本題的根本,需要知道連接三角形兩邊中點的線段叫做三角形的中位線;三角形中位線定理:三角形的中位線平行于三角形的第三邊,且等于第三邊的一半;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


科目:初中數學 來源: 題型:
【題目】某片果園有果樹80棵,現準備多種一些果樹提高果園產量,但是如果多種樹,那么樹之間的距離和每棵樹所受光照就會減少,單棵樹的產量隨之降低.若該果園每棵果樹產果y(千克),增種果樹x(棵),它們之間的函數關系如圖所示. 
(1)求y與x之間的函數關系式;
(2)在投入成本最低的情況下,增種果樹多少棵時,果園可以收獲果實6750千克?
(3)當增種果樹多少棵時,果園的總產量w(千克)最大?最大產量是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市政府大力扶持大學生創業.李明在政府的扶持下投資銷售一種進價為每件20元的護眼臺燈,銷售過程中發現,每月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數:y=﹣10x+500.
(1)設李明每月獲得利潤為w(元),求出w與x的函數關系式.
(2)如果李明想要每月獲得2000元的利潤,那么銷售單價應定為多少元?
(3)當銷售單價定為多少元時,每月可獲得最大利潤?得最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,半圓O的半徑OA=4,P是OA延長線上一點,線段OP的垂直平分線分別交OP、半圓O于B、C兩點,射線PC交半圓O于點D.設PA=x,CD=y,則能表示y與x的函數關系的圖象是( )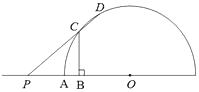
A.
B.
C.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=x+1的圖象與反比例函數y2= ![]() 的圖象交與A(1,M),B(n,﹣1)兩點,過點A作AC⊥x軸于點C,過點B作BD⊥x軸于點D,連接AO,BO.得出以下結論:
的圖象交與A(1,M),B(n,﹣1)兩點,過點A作AC⊥x軸于點C,過點B作BD⊥x軸于點D,連接AO,BO.得出以下結論:
①點A和點B關于直線y=﹣x對稱;
②當x<1時,y2>y1;
③S△AOC=S△BOD;
④當x>0時,y1 , y2都隨x的增大而增大.
其中正確的是( )
A.①②③
B.②③
C.①③
D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,拋物線l1:y=ax2﹣4ax+5+4a(a<0)的頂點為A,直線l2:y=kx+3過點A,直線l2與拋物線l1及y軸分別交于B,C.
(1)求k的值;
(2)若B為AC的中點,求a的值;
(3)在(2)的條件下,直接寫出不等式ax2﹣4ax+5+4a<kx+3的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2﹣2 ![]() ax﹣9a與坐標軸交于A,B,C三點,其中C(0,3),∠BAC的平分線AE交y軸于點D,交BC于點E,過點D的直線l與射線AC,AB分別交于點M,N.
ax﹣9a與坐標軸交于A,B,C三點,其中C(0,3),∠BAC的平分線AE交y軸于點D,交BC于點E,過點D的直線l與射線AC,AB分別交于點M,N.
(1)直接寫出a的值、點A的坐標及拋物線的對稱軸;
(2)點P為拋物線的對稱軸上一動點,若△PAD為等腰三角形,求出點P的坐標;
(3)證明:當直線l繞點D旋轉時, ![]() +
+ ![]() 均為定值,并求出該定值.
均為定值,并求出該定值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y= ![]() 與y軸交于點A,與直線y=﹣
與y軸交于點A,與直線y=﹣ ![]() 交于點B,以AB為邊向右作菱形ABCD,點C恰與原點O重合,拋物線y=(x﹣h)2+k的頂點在直線y=﹣
交于點B,以AB為邊向右作菱形ABCD,點C恰與原點O重合,拋物線y=(x﹣h)2+k的頂點在直線y=﹣ ![]() 上移動.若拋物線與菱形的邊AB、BC都有公共點,則h的取值范圍是( )
上移動.若拋物線與菱形的邊AB、BC都有公共點,則h的取值范圍是( )
A.﹣2 ![]()
B.﹣2≤h≤1
C.﹣1 ![]()
D.﹣1 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com