【題目】（1）計算：
（2）如圖，在矩形 ABCD 中，AE 平分∠BAD，交 BC 于點 E，過點 E 作 EF⊥AD 于點 F，求證：四邊形ABEF 是正方形．
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，△ABC的三個頂點的位置如圖所示，點A'的坐標是（-2，2），現將△ABC平移，使點A變換為點A'，點B'、C'分別是B、C的對應點.
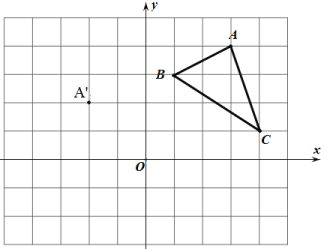
（1）直接寫出點B'、C'的坐標：B' ，C' ；并在坐標系中畫出平移后的△A'B'C'（不寫畫法）；
（2）若△ABC內部一點P的坐標為（a，b），則點P的對應點P的坐標是 ；
（3）若△ABC繞點C逆時針旋轉90°至△A1B1C，畫出△A1B1C.
（4）求△A'B'C'的面積是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有一個拋物線型蔬菜大棚，將其橫截面放在如圖所示的平面直角坐標系中，拋物線可近似用函數
來表示．已知大棚在地面上的寬度OA為8米，距離O點2米處的棚高BC為
米．
（1）求該拋物線的函數解析式；
（2）若借助橫梁DE建一個門，且要求門的高度不低于1.5米，則橫梁DE的寬度最多是多少米？（結果保留根號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，直線
與
軸、
軸分別交于
、
兩點，兩動點
、
分別以
個單位長度/秒和
個單位長度/秒的速度從、兩點同時出發向
點運動（運動到點停止）；過點作
交拋物線
于、
兩點，交
于點
，連結
、
．若拋物線的頂點
恰好在上且四邊形
是菱形，則
、
的值分別為（ ）
A. 
、
B. 、
C. 
、 D. 、
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】先化簡，再求值：(1)(2x+y)2+(x-y)(x+y)-5x(x-y)，其中x=
+1，y=-1.
(2)[(x+2y)2-(x+y)(3x-5y)-5y2]÷2x，其中x=-2，y=
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y=-x-2交x軸于點A，交y軸于點B，拋物線y=ax2+bx+c的頂點為A，且經過點B．
（1）求該拋物線的解析式；
（2）若點C（m，–
）在拋物線上，求m的值．
（3）根據圖象直接寫出一次函數值大于二次函數值時x 的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,等邊△OAB和等邊△AFE的一邊都在x軸上,雙曲線
經過邊OB的中點C和AE的中點D.已知等邊△OAB的邊長為4,則等邊△AEF的邊長為______.
．
查看答案和解析>>
科目：初中數學 來源： 題型：
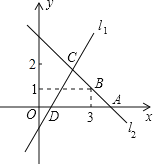
【題目】如圖，直線l1：y＝2x﹣2與x軸交于點D，直線l2：y＝kx+b與x軸交于點A，且經過點B，直線l1，l2交于點C（m，2）．
（1）求m的值；
（2）求直線l2的解析式；
（3）根據圖象，直接寫出1＜kx+b＜2x﹣2的解集．
（4）求△ACD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
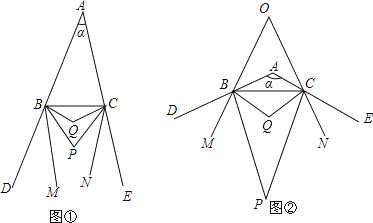
【題目】已知如圖①，BP、CP分別是△ABC的外角∠CBD、∠BCE的角平分線，BQ、CQ分別是∠PBC、∠PCB的角平分線，BM、CN分別是∠PBD、∠PCE的角平分線，∠BAC＝α．
（1）當α＝40°時，∠BPC＝ °，∠BQC＝ °；
（2）當α＝ °時，BM∥CN；
（3）如圖②，當α＝120°時，BM、CN所在直線交于點O，求∠BOC的度數；
（4）在α＞60°的條件下，直接寫出∠BPC、∠BQC、∠BOC三角之間的數量關系： ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
