
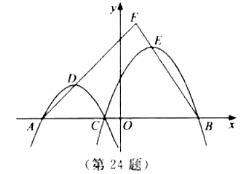
【題目】如圖,在平面直角坐標系![]() 中,已知
中,已知![]() ,
,![]() 兩點的坐標分別為
兩點的坐標分別為![]() ,
,![]() ,
,![]() 是線段
是線段![]() 上一點(與
上一點(與![]() ,
,![]() 點不重合),拋物線
點不重合),拋物線![]()
![]() (
(![]() )經過點
)經過點![]() ,
,![]() ,頂點為
,頂點為![]() ,拋物線
,拋物線![]()
![]() (
(![]() )經過點
)經過點![]() ,
,![]() ,頂點為
,頂點為![]() ,
,![]() ,
,![]() 的延長線相交于點
的延長線相交于點![]() .
.
(1)若![]() ,
,![]() ,求拋物線
,求拋物線![]() ,
,![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)是否存在這樣的實數![]() (
(![]() ),無論
),無論![]() 取何值,直線
取何值,直線![]() 與
與![]() 都不可能互相垂直?若存在,請直接寫出
都不可能互相垂直?若存在,請直接寫出![]() 的兩個不同的值;若不存在,請說明理由.
的兩個不同的值;若不存在,請說明理由.
【答案】(1)拋物線L1的解析式為y=![]() ,拋物線L2的解析式為y=
,拋物線L2的解析式為y=![]() (2)m=±2
(2)m=±2![]() (3)存在
(3)存在
【解析】
試題分析:(1)把a、m代入得到已知點,把點代入函數的解析式,然后構成方程組,根據待定系數法可求出函數的解析式;
(2)如圖,過點D作DG⊥x軸于點G,過點E作EH⊥x軸于點H,把a=-1代入函數解析式,然后結合(m,0)和(-4,0)代入可求解出函數解析式L1,然后分別求出D點坐標,得到DG、AG的長,同理得到L2,求得EH,BH的長,再根據三角形相似的判定與性質構造方程求解即可;
(3)根據前面的解答,直接寫出即可.
試題解析:(1)由題意得
解得
所以拋物線L1的解析式為y=![]()
同理,
解得
∴所以拋物線L2的解析式為y=![]()
(2)如圖,過點D作DG⊥x軸于點G,過點E作EH⊥x軸于點H
由題意得
解得
∴拋物線L1的解析式為y=-x2+(m-4)x+4m
∴點D的坐標為(![]() ,
,![]() )
)
∴DG=![]() ,AG=
,AG=![]()
同理可得,拋物線L2的解析式為y=-x2+(m+4)x-4m
EH=![]() ,BH=
,BH=![]()

∵AF⊥BF,DG⊥x軸,EH⊥x軸
∴∠AFB=∠AGD=∠EHB=90°
∴∠ADG=∠ABF=90°-∠BAF
∴△ADG∽△EBH
∴![]()
∴
解得m=±2![]()
(3)存在,例如:a=-![]() ,a=-
,a=-![]() .(答案不唯一)
.(答案不唯一)


科目:初中數學 來源: 題型:
【題目】端午節放假期間,小明和小華準備到宜賓的蜀南竹海(記為A)、興文石海(記為B)、夕佳山民居(記為C)、李莊古鎮(記為D)的一個景點去游玩,他們各自在這四個景點中任選一個,每個景點都被選中的可能性相同.
(1)小明選擇去蜀南竹海旅游的概率為 .
(2)用樹狀圖或列表的方法求小明和小華都選擇去興文石海旅游的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現定義一種新運算“*”,規定a*b=ab+a﹣b,如1*3=1×3+1﹣3,則﹣2*5等于( )
A. 17B. 15C. ﹣17D. ﹣15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形![]() 的對角線
的對角線![]() ,
,![]() 相交于點
相交于點![]() .
.
(1)如圖1,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的點,
上的點,![]() 與
與![]() 的延長線相交于點
的延長線相交于點![]() .若
.若![]() ,求證:
,求證:![]() ;
;
(2)如圖2,![]() 是
是![]() 上的點,過點
上的點,過點![]() 作
作![]() ,交線段
,交線段![]() 于點
于點![]() ,連結
,連結![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() .若
.若![]() ,
,
①求證:![]() ;
;
②當![]() 時,求
時,求![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一段筆直的公路AC長20千米,途中有一處休息點B,AB長15千米,甲、乙兩名長跑愛好者同時從點A出發,甲以15千米/時的速度勻速跑至點B,原地休息半小時后,再以10千米/時的速度勻速跑至終點C;乙以12千米/時的速度勻速跑至終點C,下列選項中,能正確反映甲、乙兩人出發后2小時內運動路程y(千米)與時間x(小時)函數關系的圖象是( )
A.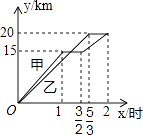
B.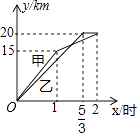
C.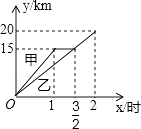
D.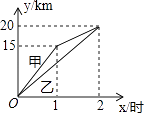
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y=2x+3與y軸交于點A,直線y=kx﹣1與y軸交于點B,與直線y=2x+3交于點C(﹣1,n).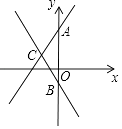
(1)求n、k的值;
(2)求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com