
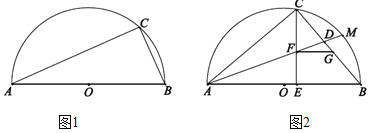
【題目】已知AB是半圓O的直徑,點C在半圓O上.
(1)如圖1,若AC=3,∠CAB=30°,求半圓O的半徑;
(2)如圖2,M是![]() 的中點,E是直徑AB上一點,AM分別交CE,BC于點F,D. 過點F作FG∥AB交邊BC于點G,若△ACE與△CEB相似,請探究以點D為圓心,GB長為半徑的⊙D與直線AC的位置關系,并說明理由.
的中點,E是直徑AB上一點,AM分別交CE,BC于點F,D. 過點F作FG∥AB交邊BC于點G,若△ACE與△CEB相似,請探究以點D為圓心,GB長為半徑的⊙D與直線AC的位置關系,并說明理由.
【答案】(1)半圓O的半徑為![]() ;
;
(2)⊙D與直線AC相切,理由見解析
【解析】試題分析:(1)依據直徑所對的圓周角是直角可得∠C=90°,2再依據三角函數即可求解;(2) 依據△ACE與△CEB相似證出∠AEC=∠CEB=90°, 再依據M是![]() 的中點,證明CF=CD, 過點F作FP∥GB交于AB于點P, 證出△ACF≌△APF,得出CF=FP,再證四邊形FPBG是平行四邊形,得到 FP=GB從而CD=GB,點D到直線AC的距離為線段CD的長.
的中點,證明CF=CD, 過點F作FP∥GB交于AB于點P, 證出△ACF≌△APF,得出CF=FP,再證四邊形FPBG是平行四邊形,得到 FP=GB從而CD=GB,點D到直線AC的距離為線段CD的長.
試題解析:
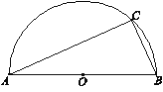
(1)∵ AB是半圓O的直徑,
∴ ∠C=90°.
在Rt△ACB中,AB=![]()
=![]()
=2![]() .
.
∴ OA=![]()
(2)
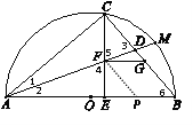
⊙D與直線AC相切.
理由如下:
由(1)得∠ACB=90°.
∵ ∠AEC=∠ECB+∠6,
∴ ∠AEC>∠ECB,∠AEC>∠6.
∵ △ACE與△CEB相似,
∴ ∠AEC=∠CEB=90°.
在Rt△ACD,Rt△AEF中分別有
∠1+∠3=90°,∠2+∠4=90°.
∵ M是![]() 的中點,
的中點,
∴ ∠COM=∠BOM.
∴ ∠1=∠2,
∴ ∠3=∠4.
∵ ∠4=∠5,
∴ ∠3=∠5.
∴ CF=CD.
過點F作FP∥GB交于AB于點P,則∠FPE=∠6.
在Rt△AEC,Rt△ACB中分別有
∠CAE+∠ACE=90°,∠CAE+∠6=90°.
∴ ∠ACE=∠6=∠FPE.
又∵ ∠1=∠2,AF=AF,
∴ △ACF≌△APF.
∴ CF=FP.
∵ FP∥GB,FG∥AB,
∴ 四邊形FPBG是平行四邊形.
∴ FP=GB.
∴ CD=GB.
∵ CD⊥AC,
∴ 點D到直線AC
∴ ⊙D與直線AC相切.


科目:初中數學 來源: 題型:
【題目】定下面一列分式: ![]() (其中x≠0)
(其中x≠0)
(1)把任意一個分式除以前面一個分式,你發現了什么規律?
(2)根據你發現的規律,試寫出給定的那列分式中的第7個分式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知D、E在△ABC的邊上,DE∥BC,∠B=60°,∠AED=40°,則∠A的度數為( ) 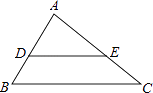
A.100°
B.90°
C.80°
D.70°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)0﹣3﹣(﹣4)+2
(2)﹣22+3×(﹣1)4﹣(﹣4)×5
(3)( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣18)
)×(﹣18)
(4)(﹣5)×(﹣3 ![]() )+(﹣7)×(﹣3
)+(﹣7)×(﹣3 ![]() )+2×(﹣3
)+2×(﹣3 ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
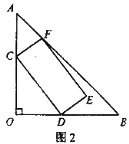
【題目】在△AOB中,OA=OB=8,∠AOB=90°,矩形CDEF的頂點C、D、F分別在邊AO、OB、AB上。
(1)如圖1,若C、D恰好是邊AO、OB的中點,則此時矩形CDEF的面積為_________;
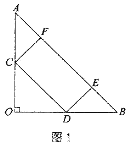
(2)如圖2,若![]() =
=![]() ,求矩形CDEF面積的最大值。
,求矩形CDEF面積的最大值。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有這樣一個問題:探究函數y=![]() 的圖象與性質。小慧根據學習函數的經驗,對函數y=
的圖象與性質。小慧根據學習函數的經驗,對函數y=![]() 的圖象與性質進行了探究。下面是小慧的探究過程,請補充完成:
的圖象與性質進行了探究。下面是小慧的探究過程,請補充完成:
(1)函數y=![]() 的自變量x的取值范圍是__________;
的自變量x的取值范圍是__________;
(2)列出y與x的幾組對應值。請直接寫出m的值,m=________;
x | … | -3 | -2 | 0 | 1 | 1.5 | 2.5 | m | 4 | 6 | 7 | … |
y | … | 2.4 | 2.5 | 3 | 4 | 6 | -2 | 0 | 1 | 1.5 | 1.6 | … |
(3)請在平面直角坐標系xOy中,描出以上表中各對對應值為坐標的點,并畫出該函數的圖象;
(4)結合函數的圖象,寫出該函數的兩條性質:
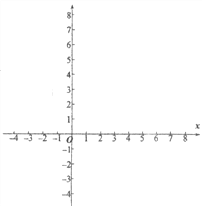
①_____________________________________________;
②____________________________________________。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com