
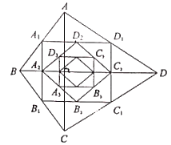
【題目】如圖,四邊形![]() 中,
中,![]() 順次連接四邊形
順次連接四邊形![]() 各邊中點,得到四邊形
各邊中點,得到四邊形![]() ,再順次連接四邊形
,再順次連接四邊形![]() 各邊中點,得到四邊形
各邊中點,得到四邊形![]() ...如此進行下去,得到四邊形
...如此進行下去,得到四邊形![]() 則下列結論正確的個數有( )
則下列結論正確的個數有( )
①四邊形![]() 是矩形;②四邊形
是矩形;②四邊形![]() 是菱形;③四邊形
是菱形;③四邊形![]() 的周長為
的周長為![]() ; ④四邊形
; ④四邊形![]() 的面積是
的面積是![]() .
.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
【答案】A
【解析】
首先根據題意,找出變化后的四邊形的邊長與四邊形ABCD中各邊長的長度關系規律,然后對以下選項作出分析與判斷:
①根據矩形的判定與性質作出判斷;
②根據菱形的判定與性質作出判斷;
③由四邊形的周長公式:周長=邊長之和,來計算四邊形A5B5C5D5的周長;
④根據四邊形AnBnCnDn的面積與四邊形ABCD的面積間的數量關系來求其面積.
解:如下圖,連接連接A1C1,B1D1,
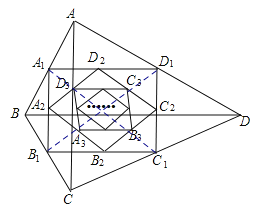
∵在四邊形ABCD中,順次連接四邊形ABCD各邊中點,得到四邊形A1B1C1D1,
∴A1D1∥BD,B1C1∥BD,C1D1∥AC,A1B1∥AC;
∴A1D1∥B1C1,A1B1∥C1D1,
∴四邊形A1B1C1D1是平行四邊形,
∵AC丄BD,
∴四邊形A1B1C1D1是矩形,故①正確;
∴B1D1=A1C1(矩形的兩條對角線相等);
∴A2D2=C2D2=C2B2=B2A2(中位線定理),
∴四邊形A2B2C2D2是菱形;
依次類推,可知當n為奇數時四邊形AnBnCnDn是矩形,當n為偶數時四邊形AnBnCnDn是菱形,故②正確;
根據中位線的性質可知,![]() ,
,
∴四邊形A5B5C5D5的周長是![]() ,
,
故③正確;
∵四邊形ABCD中,AC=a,BD=b,且AC丄BD,
∴S四邊形ABCD=ab÷2;
由三角形的中位線的性質可以推知,每得到一次四邊形,它的面積變為原來的一半,
四邊形AnBnCnDn的面積是![]() ,
,
故④正確;
綜上所述,①②③④正確.
故選:A.


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:初中數學 來源: 題型:
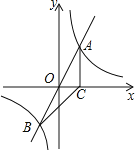
【題目】如圖, 正比例函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于A、B兩點,過點A作AC垂直x軸于點C,連接BC,若ΔABC面積為 2.
的圖象交于A、B兩點,過點A作AC垂直x軸于點C,連接BC,若ΔABC面積為 2.
(1)求k的值
(2)x軸上是否存在一點D,使ΔABD是以AB為斜邊的直角三角形?若存在,求出點D的坐標,若不存在,說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系第一象限中,已知點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,點
,點![]() 坐標為
坐標為![]() ,動點
,動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度勻速向點
個單位長度的速度勻速向點![]() 方向運動,與此同時,
方向運動,與此同時,![]() 軸上動點
軸上動點![]() 從點
從點![]() 出發,以相同的速度向右運動, 兩動點運動時間為:
出發,以相同的速度向右運動, 兩動點運動時間為:![]() , 以
, 以![]() 分別為邊作矩形
分別為邊作矩形![]() , 過點
, 過點![]() 作雙曲線交線段
作雙曲線交線段![]() 于點
于點![]() ,作
,作![]() 中點
中點![]() ,連接
,連接![]()
(1)當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
(2)若![]() 平分
平分![]() , 則
, 則![]() 的值為多少?
的值為多少?
(3)若![]() 為直角, 則
為直角, 則![]() 的值為多少?
的值為多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,BD⊥AC,AE⊥BC,AE、BD交于點O,連接CO,∠ABC=54°,∠ACB=48°,則∠COD=( )

A. 51°B. 66°C. 78°D. 88°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某醫藥研究所開發了一種新藥,在實際驗藥時發現,如果成人按規定劑量服用,那么每毫升血液中含藥量![]() (毫克)隨時間
(毫克)隨時間![]() (小時)的變化情況如圖所示,當成年人按規定劑量服藥后.
(小時)的變化情況如圖所示,當成年人按規定劑量服藥后.

(1)當![]() 時,
時,![]() 與
與![]() 之間的函數關系式是________;
之間的函數關系式是________;
(2)當![]() 時,
時,![]() 與
與![]() 之間的函數關系式是______;
之間的函數關系式是______;
(3)如果每毫升血液中含藥量![]() 毫克或
毫克或![]() 毫克以上時,治療疾病最有效,那么這個有效時間范圍是_______小時.
毫克以上時,治療疾病最有效,那么這個有效時間范圍是_______小時.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們定義:等腰三角形中底邊與腰的比叫作底角的鄰對(can).如圖①,在△ABC中,AB=AC,底角∠B的鄰對記作canB,這時canB=![]() .容易知道一個角的大小與這個角的鄰對值是一一對應的,根據上述角的鄰對的定義,解下列問題:
.容易知道一個角的大小與這個角的鄰對值是一一對應的,根據上述角的鄰對的定義,解下列問題:
(1) . can30°=______ __;
(2) . 如圖②,已知在△ABC中,AB=AC,canB=![]() ,S△ABC=24,求△ABC的周長.
,S△ABC=24,求△ABC的周長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在東營市中小學標準化建設工程中,某學校計劃購進一批電腦和電子白板,經過市場考察得知,購買1臺電腦和2臺電子白板需要3.5萬元,購買2臺電腦和1臺電子白板需要2.5萬元.
(1)求每臺電腦、每臺電子白板各多少萬元?
(2)根據學校實際,需購進電腦和電子白板共30臺,總費用不超過30萬元,但不低于28萬元,請你通過計算求出有幾種購買方案,哪種方案費用最低.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某校數學興趣小組利用自制的直角三角形硬紙板DEF來測量操場旗桿AB的高度,他們通過調整測量位置,使斜邊DF與地面保持平行,并使邊DE與旗桿頂點A在同一直線上,已知DE=0.5米,EF=0.25米,目測點D到地面的距離DG=1.5米,到旗桿的水平距離DC=20米,求旗桿的高度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,BD的垂直平分線交AD于E,交BC于F,連接BE 、DF.

(1)判斷四邊形BEDF的形狀,并說明理由;
(2)若AB=8,AD=16,求BE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com