
【題目】如圖,Rt△ABC中,∠ACB=90°.
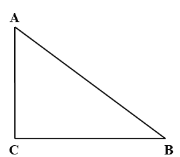
(1)作∠BAC的平分線,交BC于點D;(要求:尺規作圖,不寫作法,保留作圖痕跡)
(2)在(1)的條件下,若BD=5,CD=3,求AC的長.
【答案】(1)見解析;(2)6.
【解析】
(1)先以A為圓心,小于AC長為半徑畫弧,交AC,AB運用H、F;再分別以H、F為圓心,大于![]() HF長為半徑畫弧,兩弧交于點M,最后畫射線AM交CB于D;
HF長為半徑畫弧,兩弧交于點M,最后畫射線AM交CB于D;
(2)過點D作DE⊥AB,垂足為E,先證明△ACD≌△AED得到AC=AE,CD=DE=3,再由勾股定理得求的BE長,然后在Rt△ABC中,設AC=x,則AB=AE+BE=x+4,最后再次運用勾股定理求解即可.
解:(1)如圖:
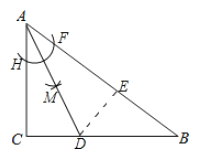
(2)過點D作DE⊥AB,垂足為E.則∠AED=∠BED=90°
∵AD平分∠BAC
∴CD=DE
在RtACD和RtAED中
CD=DE,AD=AD
∴ △CDE≌△AED(HL)
∴AC=AE,CD=DE=3
在Rt△BDE中,
由勾股定理得:DE2+BE2=BD2
∴BE2=BD2-DE2=52-32=16.
∴BE=4
在Rt△ABC中,設AC=x,則AB=AE+BE=x+4.
由勾股定理得:AC2+BC2=AB2,即x2+82=(x+4)2
解得:x=6,即AC=6.


科目:初中數學 來源: 題型:
【題目】為落實黨中央“長江大保護”新發展理念,我市持續推進長江岸線保護,還洞庭湖和長江水清岸綠的自然生態原貌.某工程隊負責對一面積為33000平方米的非法砂石碼頭進行拆除,回填土方和復綠施工,為了縮短工期,該工程隊增加了人力和設備,實際工作效率比原計劃每天提高了20%,結果提前11天完成任務,求實際平均每天施工多少平方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() ,以點
,以點![]() 為圓心,8為半徑的圓與
為圓心,8為半徑的圓與![]() 軸交于
軸交于![]() ,
,![]() 兩點,過
兩點,過![]() 作直線
作直線![]() 與
與![]() 軸負方向相交成
軸負方向相交成![]() 的角,且交
的角,且交![]() 軸于
軸于![]() 點,以點
點,以點![]() 為圓心的圓與
為圓心的圓與![]() 軸相切于點
軸相切于點![]() .
.

(1)求直線![]() 的解析式;
的解析式;
(2)將![]() 以每秒1個單位的速度沿
以每秒1個單位的速度沿![]() 軸向左平移,當
軸向左平移,當![]() 第一次與
第一次與![]() 外切時,求
外切時,求![]() 平移的時間.
平移的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】商店只有雪碧、可樂、果汁、奶汁四種飲料,每種飲料數量充足,某同學去該店購買飲料,每種飲料被選中的可能性相同.
(1)若他去買一瓶飲料,則他買到奶汁的概率是 ;
(2)若他兩次去買飲料,每次買一瓶,且兩次所買飲料品種不同,請用樹狀圖或列表法求出他恰好買到雪碧和奶汁的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用適當的方法解下列方程:
(1) x2﹣5x﹣6=0;
(2) (1﹣x)2﹣1=![]() ;
;
(3) 8x(x+2)=3x+6;
(4)(y+![]() )(y-
)(y-![]() )=20.
)=20.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一長方形紙片![]() 放在平面直角坐標系中,
放在平面直角坐標系中,![]() ,
,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發以每秒1個單位長度的速度沿
出發以每秒1個單位長度的速度沿![]() 向終點
向終點![]() 運動,運動
運動,運動![]() 秒時,動點
秒時,動點![]() 從點
從點![]() 出發以相同的速度沿
出發以相同的速度沿![]() 向終點
向終點![]() 運動,當點
運動,當點![]() 、
、![]() 其中一點到達終點時,另一點也停止運動.
其中一點到達終點時,另一點也停止運動.
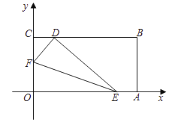
設點![]() 的運動時間為
的運動時間為![]() :(秒)
:(秒)
(1)![]() _________,
_________,![]() ___________(用含
___________(用含![]() 的代數式表示)
的代數式表示)
(2)當![]() 時,將
時,將![]() 沿
沿![]() 翻折,點
翻折,點![]() 恰好落在
恰好落在![]() 邊上的點
邊上的點![]() 處,求點
處,求點![]() 的坐標及直線
的坐標及直線![]() 的解析式;
的解析式;
(3)在(2)的條件下,點![]() 是射線
是射線![]() 上的任意一點,過點
上的任意一點,過點![]() 作直線
作直線![]() 的平行線,與
的平行線,與![]() 軸交于
軸交于![]() 點,設直線
點,設直線![]() 的解析式為
的解析式為![]() ,當點
,當點![]() 與點
與點![]() 不重合時,設
不重合時,設![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自動化車間計劃生產480個零件,當生產任務完成一半時,停止生產進行自動化程序軟件升級,用時20分鐘,恢復生產后工作效率比原來提高了![]() ,結果完成任務時比原計劃提前了40分鐘,求軟件升級后每小時生產多少個零件?
,結果完成任務時比原計劃提前了40分鐘,求軟件升級后每小時生產多少個零件?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com