Question

【題目】如圖，在平面直角坐標系xOy中，一次函數y=﹣ x+1的圖象與x軸、y軸分別交于點A、B，把Rt△AOB繞點A順時針旋轉角α（30°＜α＜180°），得到△AO′B′．
（1）當α=60°時，判斷點B是否在直線O′B′上，并說明理由；
（2）連接OO′，設OO′與AB交于點D，當α為何值時，四邊形ADO′B′是平行四邊形？請說明理由．

Answer 1

【答案】
（1）解；如圖1中，

∵一次函數y=﹣ x+1的圖象與x軸、y軸分別交于點A、B，

∴A（ ，0），B（0，1），

∴tan∠BAO= ，

∴∠BAO=30°，AB=2OB=2，

∵旋轉角為60°，

∴B′（ ，2 ），O′（ ， ），

設直線O′B′解析式為y=kx+b，

∴， ，解得 ，

∴直線O′B′的解析式為y= x+1，

∵x=0時，y=1，

∴點B（0，1）在直線O′B′上

（2）解；如圖2中，當α=120°時，四邊形ADO′B′是平行四邊形．

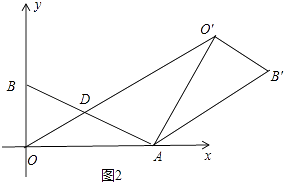
理由：∵AO=AO′，∠OAO′=120°，∠BAO=30°，

∴∠DAO′=∠AO′B′=90°，∠O′AO=∠O′AB′=30°，

∴AD∥O′B′，DO′∥AB′，

∴四邊形ADO′B′是平行四邊形

【解析】（1）首先證明∠BAO=30°，再求出直線O′B′的解析式即可解決問題．（2）如圖2中，當α=120°時，四邊形ADO′B′是平行四邊形．只要證明∠DAO′=∠AO′B′=90°，∠O′AO=∠O′AB′=30°，即可解決問題．
【考點精析】掌握平行四邊形的判定是解答本題的根本，需要知道兩組對邊分別平行的四邊形是平行四邊形：兩組對邊分別相等的四邊形是平行四邊形；一組對邊平行且相等的四邊形是平行四邊形；兩組對角分別相等的四邊形是平行四邊形；對角線互相平分的四邊形是平行四邊形．