
【題目】如圖,在正方形![]() 中,點(diǎn)
中,點(diǎn)![]() 在邊
在邊![]() 上(點(diǎn)
上(點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 、
、![]() 不重合),過點(diǎn)
不重合),過點(diǎn)![]() 作
作![]() ,
,![]() 與邊
與邊![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,與邊
,與邊![]() 的延長線相交于點(diǎn)
的延長線相交于點(diǎn)![]() .
.
(1)![]() 與
與![]() 有什么樣的數(shù)量關(guān)系?請直接寫出你的結(jié)論:____________________
有什么樣的數(shù)量關(guān)系?請直接寫出你的結(jié)論:____________________
(2)![]() 、
、![]() 、
、![]() 的數(shù)量之間具有怎樣的關(guān)系?并證明你所得到的結(jié)論.
的數(shù)量之間具有怎樣的關(guān)系?并證明你所得到的結(jié)論.
(3)如果正方形的邊長是1,![]() ,直接寫出點(diǎn)
,直接寫出點(diǎn)![]() 到直線
到直線![]() 的距離.
的距離.

解:(1)![]() 與
與![]() 的數(shù)量關(guān)系:____________________
的數(shù)量關(guān)系:____________________
(2)![]() 、
、![]() 、
、![]() 的數(shù)量之間的關(guān)系是 .
的數(shù)量之間的關(guān)系是 .
證明:
(3)點(diǎn)![]() 到直線
到直線![]() 的距離是 .
的距離是 .
【答案】(1)![]() ,理由見解析;(2)
,理由見解析;(2)![]() ,理由見解析;(3)
,理由見解析;(3)![]() .
.
【解析】
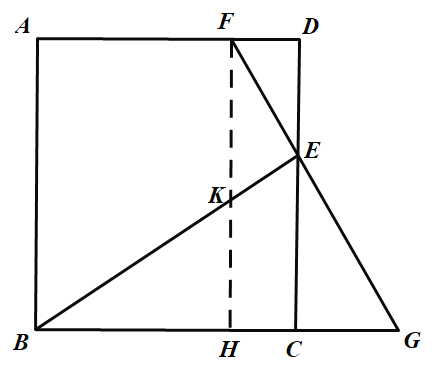
(1)過點(diǎn)F作![]() 交BE于點(diǎn)K,交BC于點(diǎn)H,根據(jù)矩形和正方形的性質(zhì)證明
交BE于點(diǎn)K,交BC于點(diǎn)H,根據(jù)矩形和正方形的性質(zhì)證明![]() ,然后即可得出
,然后即可得出![]() ;
;
(2)根據(jù)矩形的性質(zhì)有DF=CH,根據(jù)全等三角形的性質(zhì)有![]() ,則可得出結(jié)論
,則可得出結(jié)論![]() ;
;
(3)連接AE,過點(diǎn)A作![]() 交BE于點(diǎn)M,利用
交BE于點(diǎn)M,利用![]() 和
和![]() 即可求解.
即可求解.
(1)![]() ,理由如下:
,理由如下:
過點(diǎn)F作![]() 交BE于點(diǎn)K,交BC于點(diǎn)H,
交BE于點(diǎn)K,交BC于點(diǎn)H,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
∵四邊形ABCD是正方形,
![]() .
.
![]() ,
,
∴四邊形CDFH是矩形,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,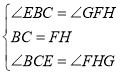
![]() ,
,
![]() ;
;
(2)![]() ,理由如下:
,理由如下:
∵四邊形CDFH是矩形,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ;
;
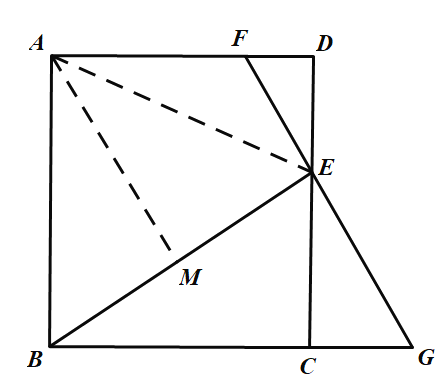
(3)如圖,連接AE,過點(diǎn)A作![]() 交BE于點(diǎn)M,
交BE于點(diǎn)M,
![]() ,
,
![]() .
.
∵正方形ABCD的邊長為1,
∴![]() .
.
![]() ,
,
![]() ,
,
∴點(diǎn)A到BE的距離為![]() .
.


 科學(xué)實(shí)驗(yàn)活動(dòng)冊系列答案
科學(xué)實(shí)驗(yàn)活動(dòng)冊系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)P是∠AOB內(nèi)任意一點(diǎn),且∠AOB=40°,點(diǎn)M和點(diǎn)N分別是射線OA和射線OB上的動(dòng)點(diǎn),當(dāng)△PMN周長取最小值時(shí),則∠MPN的度數(shù)為( )

A. 140° B. 100° C. 50° D. 40°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)P與點(diǎn) Q 都在y軸上,且關(guān)于x軸對稱.
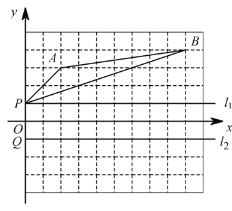
(1)請畫出△ABP 關(guān)于x軸的對稱圖形 ![]() (其中點(diǎn) A 的對稱點(diǎn)用
(其中點(diǎn) A 的對稱點(diǎn)用 ![]() 表示,點(diǎn) 的對稱點(diǎn)用
表示,點(diǎn) 的對稱點(diǎn)用 ![]() 表示);
表示);
(2)點(diǎn)P ,Q 同時(shí)都從y軸上的位置出發(fā),分別沿l1,l2方向,以相同的速度向右運(yùn)動(dòng),在運(yùn)動(dòng)過程中是否在某個(gè)位置使得![]()
![]() 成立?若存在,請你在圖中畫出此時(shí) PQ 的位置(用線段
成立?若存在,請你在圖中畫出此時(shí) PQ 的位置(用線段 ![]() 表示),若不存在,請你說明理由(注:畫圖時(shí),先用鉛筆畫好,再用鋼筆描黑).
表示),若不存在,請你說明理由(注:畫圖時(shí),先用鉛筆畫好,再用鋼筆描黑).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1.直線AD∥EF,點(diǎn)B,C分別在EF和AD上,∠A=∠ABC,BD平分∠CBF.
(1)求證:AB⊥BD;
(2)如圖2,BG⊥AD于點(diǎn)G,求證:∠ACB=2∠ABG;
(3)在(2)的條件下,如圖3,CH平分∠ACB交BG于點(diǎn)H,設(shè)∠ABG=α,請直接寫出∠BHC的度數(shù).(用含α的式子表示)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,每個(gè)小正方形的邊長都是1.![]() 均在網(wǎng)格的格點(diǎn)上.
均在網(wǎng)格的格點(diǎn)上.
(1)直接寫出四邊形![]() 的面積與
的面積與![]() 、
、![]() 的長度;
的長度;
(2)![]() 是直角嗎?請說出你的判斷理由.
是直角嗎?請說出你的判斷理由.
(3)找到一個(gè)格點(diǎn)![]() ,并畫出四邊形
,并畫出四邊形![]() ,使得其面積與四邊形
,使得其面積與四邊形![]() 的面積相等.
的面積相等.
解:(1)![]() ___________;
___________;![]() ___________;
___________;![]() ___________.
___________.
(2)判斷___________(填“是”或“否”)
理由_________________________________________________;
(3)在圖中畫出一個(gè)滿足條件的四邊形![]() .
.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,AD是中線,∠BAD=∠B+∠C,tan∠ABC=![]() ,則tan∠BAD=________.
,則tan∠BAD=________.

【答案】![]()
【解析】延長AD到E,使AD=DE,CF ![]() ,
,
在![]() 與
與![]() ,
,
,  ,所以
,所以![]() ,
,
![]()
![]() 是等腰三角形,s
是等腰三角形,s
設(shè)EM= x,DE=11,MC=10,
![]() ,
,
 ,
,
![]() x=
x=![]() ,
,
![]() tan∠BAD=
tan∠BAD=![]() .
.
故答案為![]() .
.

點(diǎn)睛:倍長中線法構(gòu)造全等三角形,如圖,AD是中線,令AD=DE,則![]() ADC全等
ADC全等![]() EBD.
EBD.

【題型】填空題
【結(jié)束】
21
【題目】先化簡,再求值: ![]() ÷(
÷(![]() -a+2),其中a=2sin60°+3tan45°.
-a+2),其中a=2sin60°+3tan45°.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 外角
外角![]() 的平分線,
的平分線,![]() .
.
(1)求證:四邊形![]() 為矩形;
為矩形;
(2)當(dāng)![]() 與
與![]() 滿足什么數(shù)量關(guān)系時(shí),四邊形
滿足什么數(shù)量關(guān)系時(shí),四邊形![]() 是正方形?并給予證明
是正方形?并給予證明

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD的邊長為1,AC,BD是對角線。將△DCB繞著點(diǎn)D順時(shí)針旋轉(zhuǎn)45°得到△DGH,HG交AB于點(diǎn)E,連接DE交AC于點(diǎn)F,連接FG。則下列結(jié)論:①四邊形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正確的結(jié)論是( )
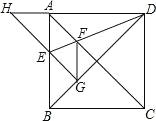
A. ①②③④ B. ①②③ C. ①② D. ②
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形![]() 中,點(diǎn)
中,點(diǎn)![]() 為對角線
為對角線![]() 的中點(diǎn),過點(diǎn)
的中點(diǎn),過點(diǎn)![]() 作
作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,連接
,連接![]() ,
,![]() .
.
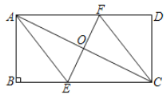
(1)求證:四邊形![]() 是菱形;
是菱形;
(2)連接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com