Question

【題目】如圖，在△ABC中，AB=AC，AB的垂直平分線交AB于點N，交BC的延長線于點M，若∠A=40°．

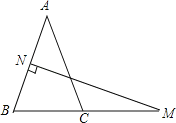
（1）求∠NMB的度數；

（2）如果將（1）中∠A的度數改為70°，其余條件不變，再求∠NMB的度數；

（3）你發現∠A與∠NMB有什么關系，試證明之．

Answer 1

【答案】（1）∠NMB=20°；（2）∠NMB =35°；（3）∠NMB=∠A，證明見解析.

【解析】試題分析：（1）由在△ABC中，AB=AC，∠A=40°，根據等腰三角形的性質，可求得∠ABC的度數，又由AB的垂直平分線交AB于點N，交BC的延長線于點M，即可求得答案；

（2）由在△ABC中，AB=AC，∠A=70°，根據等腰三角形的性質，可求得∠ABC的度數，又由AB的垂直平分線交AB于點N，交BC的延長線于點M，即可求得答案；

（3）由在△ABC中，AB=AC，根據等腰三角形的性質，即可用∠A表示出∠ABC，又由AB的垂直平分線交AB于點N，交BC的延長線于點M，即可求得答案．

試題解析：（1）∵在△ABC中，AB=AC，∠A=40°，

∴∠ABC=∠ACB=70°，

∵AB的垂直平分線交AB于點N，交BC的延長線于點M，

∴MN⊥AB，

∴∠NMB=90°∠ABC=20°；

（2）∵在△ABC中，AB=AC，∠A=70°，

∴∠ABC=∠ACB=55°，

∵AB的垂直平分線交AB于點N，交BC的延長線于點M，

∴MN⊥AB，

∴∠NMB=90°∠ABC=35°；

（3）∠NMB=∠A.

理由：∵在△ABC中，AB=AC，

∴∠ABC=∠ACB=，

∵AB的垂直平分線交AB于點N，交BC的延長線于點M，

∴MN⊥AB，

∴∠NMB=90°∠ABC=∠A.