
【題目】如圖,在數軸上![]() 點表示數
點表示數![]() ,
,![]() 點表示數
點表示數![]() ,
,![]() 表示
表示![]() 點和
點和![]() 點之間的距離,且
點之間的距離,且![]() ,
,![]() 滿足
滿足![]() .
.
![]()
(1)求![]() ,
,![]() 兩點之間的距離;
兩點之間的距離;
(2)若在數軸上存在一點![]() ,且
,且![]() ,直接寫出
,直接寫出![]() 點表示的數;
點表示的數;
(3)若在原點![]() 處放一擋板,一小球甲從點
處放一擋板,一小球甲從點![]() 處以1個單位/秒的速度向左運動;同時另一小球乙從點
處以1個單位/秒的速度向左運動;同時另一小球乙從點![]() 處以2個單位/秒的速度也向左運動,在碰到擋板后(忽略球的大小,可看作一點)以原來的速度向相反的方向運動,設運動的時間為t(秒),
處以2個單位/秒的速度也向左運動,在碰到擋板后(忽略球的大小,可看作一點)以原來的速度向相反的方向運動,設運動的時間為t(秒),
①分別表示甲、乙兩小球到原點的距離(用t表示);
②求甲、乙兩小球到原點的距離相等時經歷的時間.
【答案】(1)8;(2)![]() 或
或![]() ;(3)(3)①t+2; 6-2t;2t-6;②故當t=
;(3)(3)①t+2; 6-2t;2t-6;②故當t=![]() 秒或t=8秒時,甲乙兩小球到原點的距離相等.
秒或t=8秒時,甲乙兩小球到原點的距離相等.
【解析】
(1)先根據非負數的性質求出a、b的值,再根據兩點間的距離公式即可求得A、B兩點之間的距離;
(2)分C點在線段AB上和線段AB的延長線上兩種情況討論即可求解;
(3)①甲球到原點的距離=甲球運動的路程+OA的長,乙球到原點的距離分兩種情況:(Ⅰ)當0<t≤3時,乙球從點B處開始向左運動,一直到原點O,此時OB的長度-乙球運動的路程即為乙球到原點的距離;(Ⅱ)當t>3時,乙球從原點O處開始向右運動,此時乙球運動的路程-OB的長度即為乙球到原點的距離;
②分兩種情況:(Ⅰ)0<t≤3,(Ⅱ)t>3,根據甲、乙兩小球到原點的距離相等列出關于t的方程,解方程即可.
(1)∵|a+2|+(b+3a)2=0,
a+2=0,b+3a=0,
∴a=-2,b=6;
∴AB的距離=|b-a|=8;
(2)設數軸上點C表示的數為c.
∵AC=2BC,
∴|c-a|=2|c-b|,即|c+2|=2|c-6|.
∵AC=2BC>BC,
∴點C不可能在BA的延長線上,則C點可能在線段AB上和線段AB的延長線上.
①當C點在線段AB上時,則有-2≤c≤6,
得c+2=2(6-c),解得c=![]() ;
;
②當C點在線段AB的延長線上時,則有c>6,
得c+2=2(c-6),解得c=14.
故當AC=2BC時,c=![]() 或c=14;
或c=14;
(3)①∵甲球運動的路程為:1t=t,OA=2,
∴甲球與原點的距離為:t+2;
乙球到原點的距離分兩種情況:
(Ⅰ)當0<t≤3時,乙球從點B處開始向左運動,一直到原點O,
∵OB=6,乙球運動的路程為:2t=2t,
∴乙球到原點的距離為:6-2t;
(Ⅱ)當t>3時,乙球從原點O處開始一直向右運動,
此時乙球到原點的距離為:2t-6;
②當0<t≤3時,得t+2=6-2t,
解得t=![]() ;
;
當t>3時,得t+2=2t-6,
解得t=8.
故當t=![]() 秒或t=8秒時,甲乙兩小球到原點的距離相等.
秒或t=8秒時,甲乙兩小球到原點的距離相等.


科目:初中數學 來源: 題型:
【題目】如圖,邊長為2的正方形紙片ABCD中,點M為邊CD上一點(不與C,D重合),將△ADM沿AM折疊得到△AME,延長ME交邊BC于點N,連結AN.
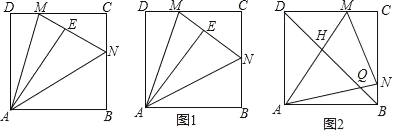
(1)猜想∠MAN的大小是否變化,并說明理由;
(2)如圖1,當N點恰為BC中點時,求DM的長度;
(3)如圖2,連結BD,分別交AN,AM于點Q,H.若BQ=![]() ,求線段QH的長度.
,求線段QH的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 請閱讀下列材料,并解答相應的問題:
將若干個數組成一個正方形數陣,若任意一行,一列及對角線上的數字之和都相等,則稱具有這種性質的數字方陣為“幻方”中國古代稱“幻方”為“河圖“、“洛書“等,例如,下面是三個三階幻方,是將數字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每條對角線上的三個數之和相等.
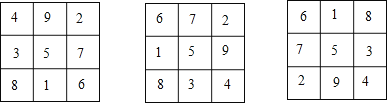
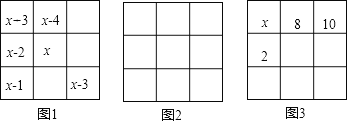
(1)設圖1的三階幻方中間的數字是x,用x的代數式表示幻方中9個數的和為 ;
(2)請你將下列九個數:﹣10、﹣8、﹣6、﹣4、﹣2、0、2、4、6分別填入圖2方格中,使得每行、每列、每條對角線上的三個數之和都相等;
(3)圖3是一個三階幻方,那么標有x的方格中所填的數是 ;
(4)如圖4所示的每一個圓中分別填寫了1、2、3…19中的一個數字(不同的圓中填寫的數字各不相同),使得圖中每一個橫或斜方向的線段上幾個圓內的數之和都相等,現在已知該圖中七個圓內的數字,則圖中的x= ,y= .

查看答案和解析>>
科目:初中數學 來源: 題型:
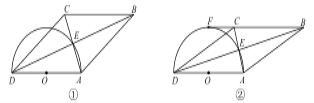
【題目】四邊形 ABCD 的對角線交于點 E,且 AE=EC,BE=ED,以 AD 為直徑的半圓過點 E,圓心 為 O.
(1)如圖①,求證:四邊形 ABCD 為菱形;
(2)如圖②,若 BC 的延長線與半圓相切于點 F,且直徑 AD=6,求弧AE 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,回答下列問題:
數軸是學習有理數的一種重要工具,任何有理數都可以用數軸上的點表示,這樣能夠運用數形結合的方法解決一些問題。例如,兩個有理數在數軸上對應的點之間的距離可以用這兩個數的差的絕對值表示;
在數軸上,有理數3與1對應的兩點之間的距離為|31|=2;
在數軸上,有理數5與2對應的兩點之間的距離為|5(2)|=7;
在數軸上,有理數2與3對應的兩點之間的距離為|23|=5;
在數軸上,有理數8與5對應的兩點之間的距離為|8(5)|=3;……
如圖1,在數軸上有理數a對應的點為點A,有理數b對應的點為點B,A,B兩點之間的距離表示為|ab|或|ba|,記為|AB|=|ab|=|ba|.

(1)數軸上有理數10與5對應的兩點之間的距離等于___;數軸上有理數x與5對應的兩點之間的距離用含x的式子表示為___;若數軸上有理數x與1對應的兩點A,B之間的距離|AB|=2,則x等于___;
(2)如圖2,點M,N,P是數軸上的三點,點M表示的數為4,點N表示的數為2,動點P表示的數為x.
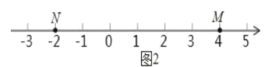
①若點P在點M,N之間,則|x+2|+|x4|=___;若|x+2|+|x4|═10,則x=___;
②根據閱讀材料及上述各題的解答方法,|x+2|+|x|+|x2|+|x4|的最小值等于___.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著互聯網的普及,某手機廠商采用先網絡預定,然后根據訂單量生產手機的方式銷售,2015年該廠商將推出一款新手機,根據相關統計數據預測,定價為2200元,日預訂量為20000臺,若定價每減少100元,則日預訂量增加10000臺.
(1)設定價減少x元,預訂量為y臺,寫出y與x的函數關系式;
(2)若每臺手機的成本是1200元,求所獲的利潤w(元)與x(元)的函數關系式,并說明當定價為多少時所獲利潤最大;
(3)若手機加工廠每天最多加工50000臺,且每批手機會有5%的故障率,通過計算說明每天最多接受的預訂量為多少?按最大量接受預訂時,每臺售價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 的對角線
的對角線![]() 交于點
交于點![]() ,直角三角形
,直角三角形![]() 繞點
繞點![]() 按逆時針旋轉,
按逆時針旋轉,![]()
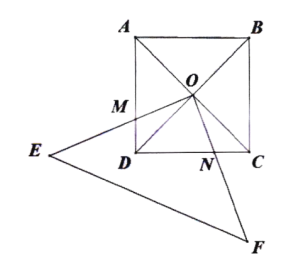
(1)若直角三角形繞點![]() 逆時針轉動過程中分別交
逆時針轉動過程中分別交![]() 兩邊于
兩邊于![]() 兩點
兩點
①求證:![]() ;
;
②連接![]() ,那么
,那么![]() 有什么樣的關系?試說明理由
有什么樣的關系?試說明理由
(2)若正方形的邊長為2,則正方形![]() 與
與![]() 兩個圖形重疊部分的面積為多少?(不需寫過程直接寫出結果)
兩個圖形重疊部分的面積為多少?(不需寫過程直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“元旦”期間,某文具店購進100只兩種型號的文具進行銷售,其進價和售價如下
型號 | 進價(元/只) | 售價(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)該店用1300元可以購進A,B兩種型號的文具各多少只?
(2)若把所購進A,B兩種型號的文具全部銷售完,利潤率超過40%沒有?請你說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com