
【題目】我們知道,在數軸上,|a|表示數a到原點的距離,這是絕對值的幾何意義.進一步地,數軸上兩個點A、B,分別用a,b表示,那么A、B兩點之間的距離為:AB=|a-b|.利用此結論,回答以下問題:
(1)數軸上表示2和5的兩點的距離是 ,數軸上表示-20和-5的兩點之間的距離是 ,數軸上表示15和-30的兩點之間的距離是 .
(2)數軸上表示x和-1的兩點A,B之間的距離是 ,如果|AB|=2,那么x是
(3)式子|x+1|+|x-2|+|x-3|的最小值是 .
【答案】(1)3,15,45;(2)|x+1|,1或-3;(3)4.
【解析】
(1)直接根據數軸上A、B兩點之間的距離|AB|=|a-b|.代入數值計算即可求任意兩點間的距離;
(2)根據兩點間的距離,分兩種情況求解即可;
(3)根據|x-a|表示數軸上x與a之間的距離,因而原式表示:數軸上一點到-1,2和3距離的和,可知當x=2時有最小值.
解:(1)數軸上表示2和5的兩點之間的距離是|2-5|=3,數軸上表示-20和-5的兩點之間的距離是|-20-(-5)|=15.數軸上表示15和-30的兩點之間的距離是|15-(-30)|=45;
(2)數軸上表示x和-1的兩點A和B之間的距離是|x-(-1)|=|x+1|,如果|AB|=2,那么x+1=2或x+1=-2,∴x為1或-3;
(3)如圖,當x表示的點在B點時,點B到點A、點B、點C距離之和最小,此時距離之和等于線段AB的長,
∴|x+1|+|x-2|+|x-3|表示數軸上一點到-1,2和3距離的和,最小值是4.

故答案為:(1)3,15,40;(2)|x+1|,1或-3;(3)4.


科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,對角線AC與BD相交于點O,不能判斷四邊形ABCD是平行四邊形的是( )

A.AB=DC,AD=BCB.AB∥DC,AD∥BC
C.AB∥DC,AD=BCD.OA=OC,OB=OD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算
(1)12-(-18)+(-7)-15
(2)(-2.7)+(+1![]() )-(-6.7)+(-1.6)
)-(-6.7)+(-1.6)
(3)20+(-14)-(-18)-13
(4)81÷|-2![]() |×
|×![]()
(5)![]()
(6)-14-(1-0.5×![]() )×(2-23)
)×(2-23)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D是∠AOB的平分線OC上任意一點,過D作DE⊥OB于E,以DE為半徑作⊙D,
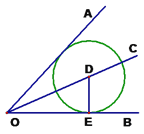
①判斷⊙D與OA的位置關系, 并證明你的結論。
②通過上述證明,你還能得出哪些等量關系?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數填入相應集合的括號內
+8.5, 0, -3.4, 12, -9, ![]() , 3.1415, -1.2,
, 3.1415, -1.2,![]() ,
, ![]()
(1)正數集合 { }
(2)整數集合 { }
(3)負分數集合 { }
(4)非正整數集合{ }
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD中,∠B=60°,AB=2cm,E、F分別是BC、CD的中點,連接AE、EF、AF,則△AEF的周長為( )

A.2![]() cmB.3
cmB.3![]() cmC.4
cmC.4![]() cmD.3cm
cmD.3cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y1=k1x+b 與反比例函數![]() 的圖象交于點A(2,m)和B(﹣6,﹣2),與y軸交于點C.
的圖象交于點A(2,m)和B(﹣6,﹣2),與y軸交于點C.
(1)y1=___,y2= ;
(2)根據函數圖象可知,當 y1<y2時,x的取值范圍是 ;
(3)過點A作AD⊥x軸于點D,求△ABD的面積.
(4)點P是反比例函數圖象上一點,△POD的面積是5,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實驗數據顯示,一般成人喝半斤低度白酒后,1.5時內其血液中酒精含量y(毫克/百毫升)與時間x (時)的關系可近似地用二次函數y=-200x2+400x刻畫;1.5時后(包括1.5時)y與x可近似地用反比例函數![]() (k>0)刻畫(如圖所示).
(k>0)刻畫(如圖所示).
(1)根據上述數學模型計算:喝酒后幾時血液中的酒精含量達到最大值?最大值為多少
(2)按國家規定,車輛駕駛人員血液中的酒精含量大于或等于20毫克/百毫升時屬于“酒后駕駛”,不能駕車上路.參照上述數學模型,假設某駕駛員晚上20:30在家喝完半斤低度白酒,第二天早上7:00能否駕車去上班?請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com