
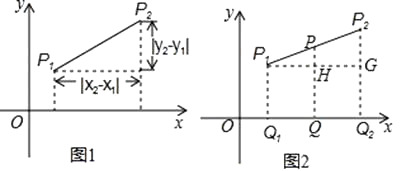
【題目】小明在求同一坐標(biāo)軸上兩點(diǎn)間的距離時發(fā)現(xiàn),對于平面直角坐標(biāo)系內(nèi)任意兩點(diǎn)P1(x1 , y1),P2(x2 , y2),可通過構(gòu)造直角三角形利用圖1得到結(jié)論:P1P2= ![]() 他還利用圖2證明了線段P1P2的中點(diǎn)P(x,y)P的坐標(biāo)公式:x=
他還利用圖2證明了線段P1P2的中點(diǎn)P(x,y)P的坐標(biāo)公式:x= ![]() ,y=
,y= ![]() .
.
(1)請你幫小明寫出中點(diǎn)坐標(biāo)公式的證明過程;
(2)①已知點(diǎn)M(2,﹣1),N(﹣3,5),則線段MN長度為;
②直接寫出以點(diǎn)A(2,2),B(﹣2,0),C(3,﹣1),D為頂點(diǎn)的平行四邊形頂點(diǎn)D的坐標(biāo):;
(3)如圖3,點(diǎn)P(2,n)在函數(shù)y= ![]() x(x≥0)的圖象OL與x軸正半軸夾角的平分線上,請?jiān)贠L、x軸上分別找出點(diǎn)E、F,使△PEF的周長最小,簡要敘述作圖方法,并求出周長的最小值.
x(x≥0)的圖象OL與x軸正半軸夾角的平分線上,請?jiān)贠L、x軸上分別找出點(diǎn)E、F,使△PEF的周長最小,簡要敘述作圖方法,并求出周長的最小值.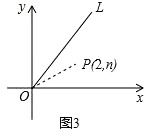
【答案】
(1)
證明:∵P1(x1,y1),P2(x2,y2),
∴Q1Q2=OQ2﹣OQ1=x2﹣x1,
∴Q1Q= ![]() ,
,
∴OQ=OQ1+Q1Q=x1+ ![]() =
= ![]() ,
,
∵PQ為梯形P1Q1Q2P2的中位線,
∴PQ= ![]() =
= ![]() ,
,
即線段P1P2的中點(diǎn)P(x,y)P的坐標(biāo)公式為x= ![]() ,y=
,y= ![]()
(2) ![]() ;(﹣3,3)或(7,1)或(﹣1,﹣3)
;(﹣3,3)或(7,1)或(﹣1,﹣3)
(3)
解:如圖,設(shè)P關(guān)于直線OL的對稱點(diǎn)為M,關(guān)于x軸的對稱點(diǎn)為N,連接PM交直線OL于點(diǎn)R,連接PN交x軸于點(diǎn)S,連接MN交直線OL于點(diǎn)E,交x軸于點(diǎn)F,
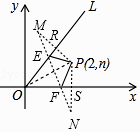
又對稱性可知EP=EM,F(xiàn)P=FN,
∴PE+PF+EF=ME+EF+NF=MN,
∴此時△PEF的周長即為MN的長,為最小,
設(shè)R(x, ![]() x),由題意可知OR=OS=2,PR=PS=n,
x),由題意可知OR=OS=2,PR=PS=n,
∴ ![]() =2,解得x=﹣
=2,解得x=﹣ ![]() (舍去)或x=
(舍去)或x= ![]() ,
,
∴R( ![]() ,
, ![]() ),
),
∴ ![]() =n,解得n=1,
=n,解得n=1,
∴P(2,1),
∴N(2,﹣1),
設(shè)M(x,y),則 ![]() =
= ![]() ,
, ![]() =
= ![]() ,解得x=
,解得x= ![]() ,y=
,y= ![]() ,
,
∴M( ![]() ,
, ![]() ),
),
∴MN= ![]() =
= ![]() ,
,
即△PEF的周長的最小值為 ![]()
【解析】(2)①∵M(jìn)(2,﹣1),N(﹣3,5),
∴MN= ![]() =
= ![]() ,
,
所以答案是: ![]() ;
;
②∵A(2,2),B(﹣2,0),C(3,﹣1),
∴當(dāng)AB為平行四邊形的對角線時,其對稱中心坐標(biāo)為(0,1),
設(shè)D(x,y),則x+3=0,y+(﹣1)=2,解得x=﹣3,y=3,
∴此時D點(diǎn)坐標(biāo)為(﹣3,3),
當(dāng)AC為對角線時,同理可求得D點(diǎn)坐標(biāo)為(7,1),
當(dāng)BC為對角線時,同理可求得D點(diǎn)坐標(biāo)為(﹣1,﹣3),
綜上可知D點(diǎn)坐標(biāo)為(﹣3,3)或(7,1)或(﹣1,﹣3),
所以答案是:(﹣3,3)或(7,1)或(﹣1,﹣3);
【考點(diǎn)精析】根據(jù)題目的已知條件,利用勾股定理的概念和軸對稱-最短路線問題的相關(guān)知識可以得到問題的答案,需要掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2;已知起點(diǎn)結(jié)點(diǎn),求最短路徑;與確定起點(diǎn)相反,已知終點(diǎn)結(jié)點(diǎn),求最短路徑;已知起點(diǎn)和終點(diǎn),求兩結(jié)點(diǎn)之間的最短路徑;求圖中所有最短路徑.


 名師點(diǎn)撥卷系列答案
名師點(diǎn)撥卷系列答案 英才計(jì)劃期末調(diào)研系列答案
英才計(jì)劃期末調(diào)研系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:在平面直角坐標(biāo)系xOy中,拋物線y=ax2+bx+c經(jīng)過點(diǎn)A(3,0),B(2,﹣3),C(0,﹣3)
(1)求拋物線的表達(dá)式;
(2)設(shè)點(diǎn)D是拋物線上一點(diǎn),且點(diǎn)D的橫坐標(biāo)為﹣2,求△AOD的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC的面積為1,分別倍長(延長一倍)AB,BC,CA得到△A1B1C1,再分別倍長A1B1,B1C1,C1A1得到△A2B2C2.…按此 規(guī)律,倍長n次后得到的△A2016B2016C2016的面積為__.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線y= ![]() x+4與x軸、y軸分別交于點(diǎn)A和點(diǎn)B,點(diǎn)C、D分別為線段AB、OB的中點(diǎn),點(diǎn)P為OA上一動點(diǎn),PC+PD值最小時點(diǎn)P的坐標(biāo)為( )
x+4與x軸、y軸分別交于點(diǎn)A和點(diǎn)B,點(diǎn)C、D分別為線段AB、OB的中點(diǎn),點(diǎn)P為OA上一動點(diǎn),PC+PD值最小時點(diǎn)P的坐標(biāo)為( )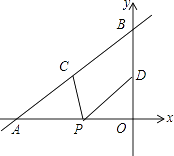
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ![]() ,0)
,0)
D.(﹣ ![]() ,0)
,0)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:在![]() 中,
中,![]() 是
是![]() 邊上的中線,點(diǎn)
邊上的中線,點(diǎn)![]() 是
是![]() 的中點(diǎn);過點(diǎn)
的中點(diǎn);過點(diǎn)![]() 作
作![]() ,交
,交![]() 的延長線于
的延長線于![]() ,連接
,連接![]() .
.
(1)求證:四邊形![]() 是平行四邊形;
是平行四邊形;
(2)當(dāng)![]() 分別滿足什么條件時,四邊形
分別滿足什么條件時,四邊形![]() 是菱形;四邊形
是菱形;四邊形![]() 是矩形,并說明理由.
是矩形,并說明理由.
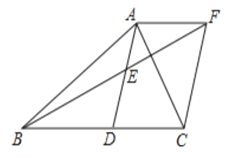
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將一幅三角板拼成如圖所示的圖形,過點(diǎn)C作CF平分∠DCE交DE于點(diǎn)F.

(1)求證:CF∥AB.
(2)求∠DFC的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,邊長為6的正六邊形ABCDEF的對稱中心與原點(diǎn)O重合,點(diǎn)A在x軸上,點(diǎn)B在反比例函數(shù)y=![]() 位于第一象限的圖象上,則k的值為( )
位于第一象限的圖象上,則k的值為( )
A.9![]()
B.9![]()
C.3![]()
D.3![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖反映的是小華從家里跑步去體育館,在那里鍛煉了一陣后又走到文具店去買筆,然后走回家,其中x表示時間,y表示小華離家的距離.根據(jù)圖像回答下列問題:
(1)小華在體育館鍛煉了_____分鐘;
(2)體育館離文具店______千米;
(3)小華從家跑步到體育館,從文具店散步回家的速度分別是多少千米/分鐘?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖在平面直角坐標(biāo)系中,A.B兩點(diǎn)的坐標(biāo)分別為(﹣2,2),(1,8),
(1)求△ABO的面積.
(2)若y軸上有一點(diǎn)M,且△MAB的面積為10.求M點(diǎn)的坐標(biāo).
(3)如圖,把直線AB以每秒2個單位的速度向右平移,運(yùn)動t秒鐘后,直線AB過點(diǎn)F(0,﹣2),此時A點(diǎn)的坐標(biāo)為 ,B點(diǎn)的坐標(biāo)為 ,過點(diǎn)A作AE⊥y軸于點(diǎn)E,過點(diǎn)B作BD⊥y軸于點(diǎn)D,請根據(jù)S△FBD=S△FAE+S梯形ABDE,求出滿足條件的運(yùn)動時間t的值.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com