
【題目】如圖,在四邊形ABCD中,AB=BC,對角線BD平分ABC,P是BD上一點,過點P作PM^AD,PN^CD,垂足分別為M、N。
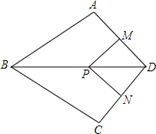
(1)求證:ADB=CDB;
(2)若ADC=90°,求證:四邊形MPND是正方形。
【答案】見解析
【解析】
試題(1)根據角平分線的性質和全等三角形的判定方法證明△ABD≌△CBD,由全等三角形的性質即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的條件可得四邊形MPND是矩形,再根據兩邊相等的四邊形是正方形即可證明四邊形MPND是正方形.
證明:(1)∵對角線BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
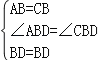 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四邊形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四邊形MPND是正方形.


科目:初中數學 來源: 題型:
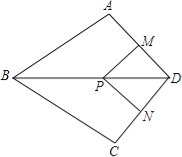
【題目】點P、Q分別是邊長為4cm的等邊![]() 的邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都是
的邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都是![]() ,設運動時間為t秒.
,設運動時間為t秒.
![]() 連接AQ、CP交于點M,則在P、Q運動的過程中,
連接AQ、CP交于點M,則在P、Q運動的過程中,![]() 變化嗎:若變化,則說明理由,若不變,則求出它的度數;
變化嗎:若變化,則說明理由,若不變,則求出它的度數;
![]() 連接PQ,
連接PQ,
![]() 當
當![]() 秒時,判斷
秒時,判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
![]() 當
當![]() 時,則
時,則![]() ______秒
______秒![]() 直接寫出結果
直接寫出結果![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,有![]() 張寫有實數的卡片,它們的背面都相同,現將它們背面朝上洗勻后如圖②擺放,從中任意翻開兩張都是無理數的概率是( )
張寫有實數的卡片,它們的背面都相同,現將它們背面朝上洗勻后如圖②擺放,從中任意翻開兩張都是無理數的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學研究課上,老師出示如圖1所示的長方形紙條![]() ,
,![]() ,
,![]() ,然后在紙條上任意畫一條截線段
,然后在紙條上任意畫一條截線段![]() ,將紙片沿
,將紙片沿![]() 折疊,
折疊,![]() 與
與![]() 交于點
交于點![]() ,得到
,得到![]() ,如圖2所示:
,如圖2所示:

(1)若![]() ,求
,求![]() 的大小;
的大小;
(2)改變折痕![]() 位置,判斷
位置,判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)愛動腦筋的小明在研究![]() 的面積時,發現
的面積時,發現![]() 邊上的高始終是個不變的值.根據這一發現,他很快研究出
邊上的高始終是個不變的值.根據這一發現,他很快研究出![]() 的面積最小值為
的面積最小值為![]() ,求
,求![]() 的大小;
的大小;
(4)小明繼續動手操作,發現了![]() 面積的最大值,請你求出這個最大值.
面積的最大值,請你求出這個最大值.

查看答案和解析>>
科目:初中數學 來源: 題型:
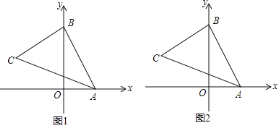
【題目】在平面直角坐標系中,![]() 的頂點坐標分別為
的頂點坐標分別為![]() ,
,![]() ,
,![]() .
.
![]() 如圖
如圖![]() ,求
,求![]() 的面積.
的面積.
![]() 若點
若點![]() 的坐標為
的坐標為![]() ,
,
①請直接寫出線段![]() 的長為________(用含
的長為________(用含![]() 的式子表示);
的式子表示);
②當![]() 時,求
時,求![]() 的值.
的值.
![]() 如圖
如圖![]() ,若
,若![]() 交
交![]() 軸于點
軸于點![]() ,直接寫出點
,直接寫出點![]() 的坐標為________.
的坐標為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=﹣ ![]() x2+bx+c與坐標軸分別交于點A(0,8)、B(8,0)和點E,動點C從原點O開始沿OA方向以每秒1個單位長度移動,動點D從點B開始沿BO方向以每秒1個單位長度移動,動點C,D同時出發,當動點D到達原點O時,點C,D停止運動.
x2+bx+c與坐標軸分別交于點A(0,8)、B(8,0)和點E,動點C從原點O開始沿OA方向以每秒1個單位長度移動,動點D從點B開始沿BO方向以每秒1個單位長度移動,動點C,D同時出發,當動點D到達原點O時,點C,D停止運動.
(1)直接寫出拋物線的解析式:;
(2)求△CED的面積S與D點運動時間t的函數解析式;當t為何值時,△CED的面積最大?最大面積是多少?
(3)當△CED的面積最大時,在拋物線上是否存在點P(點E除外),使△PCD的面積等于△CED的最大面積?若存在,求出P點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
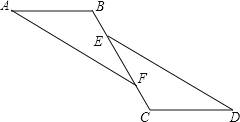
【題目】如圖,已知:點B、E、F、C在同一直線上,∠A=∠D,BE=CF,且AB∥CD.求證:AF∥ED
證明:∵BE=FC
∴BE+EF=FC+EF(____________________________)
即:___________
∵AB∥CD
∴∠B=∠C(_________________________)
在△ABF和△DCE中,
∠A=∠D, ∠B=∠C, BF=CE
∴△ABF≌△DCE(________)
∴∠AFB=∠DEC(_________________________________)
∴AF∥ED(__________________________________)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com