
【題目】如圖,在△ABC中,AC=BC,∠ACB=90°,點(diǎn)D為△ABC內(nèi)一點(diǎn),且BD=AD.
(1)求證:CD⊥AB;
(2)∠CAD=15°,E為AD延長線上的一點(diǎn),且CE=CA.
①求證:DE平分∠BDC;
②若點(diǎn)M在DE上,且DC=DM,請判斷ME、BD的數(shù)量關(guān)系,并給出證明;
③若N為直線AE上一點(diǎn),且△CEN為等腰三角形,直接寫出∠CNE的度數(shù).

【答案】(1)詳見解析;(2)①詳見解析;②:ME=BD,證明詳見解析;③∠CNE的度數(shù)為7.5°、15°、82.5°、150°.
【解析】
(1)根據(jù)中垂線的判定定理“與一條線段兩個端點(diǎn)距離相等的點(diǎn),在這條線段的垂直平分線上”可得出結(jié)論.
(2)①由∠CAD=15°,BD=AD與直角等腰三角形的性質(zhì)可知,∠DBA=∠DAB=30°,則可得∠BDE=30°+30°=60°,又根據(jù)SSS可證△ADC≌△BDC,則∠ACD=∠BCD=45°,可知∠CDE=∠ACD+∠CAD=45°+15°=60°,故DE平分∠BDC.
②連接MC,由DC=DM,∠CDE=60°,可知△MCD為等邊三角形,∠ECM=∠CMD-∠CAD=45°則根據(jù)SAS可證△BDC≌△EMC,得出結(jié)論ME=BD.
③根據(jù)題意可知,分類:當(dāng)EN=EC時;當(dāng)EN=CN時;當(dāng)CE=CN時三種情況求出∠CNE的度數(shù).
(1)證明:∵CB=CA,DB=DA,
∴CD垂直平分線段AB,
∴CD⊥AB,
故答案為:CD⊥AB.
(2)①證明:∵AC=BC,
∴∠CBA=∠CAB,
又∵∠ACB=90°,
∴∠CBA=∠CAB=45°,
又∵在△ADC和△BDC中,
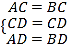 ,
,
∴△ADC≌△BDC(SSS),
∴∠CAD=∠CBD=15°,
∴∠DBA=∠DAB=30°,
∴∠BDE=30°+30°=60°,
∵∠ACB=90°,∠ACD=∠BCD,
∴∠ACD=∠BCD=45°,
∴∠CDE=∠ACD+∠CAD=45°+15°=60°,
∵∠CDE=∠BDE=60°,
∴DE平分∠BDC;
故答案為:DE平分∠BDC.
②結(jié)論:ME=BD,
理由:連接MC,

∵DC=DM,∠CDE=60°,
∴△MCD為等邊三角形,
∴CM=CD,∠CMD=60°,
又∵EC=CA,∠CAD=15°,
∴∠ECM=∠CMD-∠CAD=45°,
在△BDC和△EMC中,
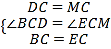 ,
,
∴△BDC≌△EMC(SAS),
∴ME=BD,
故答案為:ME=BD.
③當(dāng)EN=EC時,∠ENC=7.5°或82.5°;
當(dāng)EN=CN時,∠ENC=150°;
當(dāng)CE=CN時,∠CNE=15°,
故答案為:∠CNE的度數(shù)為7.5°、15°、82.5°、150°.


 考前必練系列答案
考前必練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(10分)如圖,已知△ABC為等邊三角形,點(diǎn)D、E分別在BC、AC邊上,且AE=CD,AD與BE相交于點(diǎn)F。

(1)求證:△ABE≌△CAD;(2)求∠BFD的度數(shù)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】綜合題:如圖1,△ABC中,∠B=30°,AB=3,BC=4,則△ABC的面積等于
(1)【回顧】
如圖1,△ABC中,∠B=30°,AB=3,BC=4,則△ABC的面積等于 . 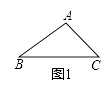
(2)【探究】
圖2是同學(xué)們熟悉的一副三角尺,一個含有30°的角,較短的直角邊長為a;另一個含有45°的角,直角邊長為b,小明用兩副這樣的三角尺拼成一個平行四邊形ABCD(如圖3),用了兩種不同的方法計(jì)算它的面積,從而推出sin75°= ![]() ,小麗用兩副這樣的三角尺拼成了一個矩形EFGH(如圖4),也推出sin75°=
,小麗用兩副這樣的三角尺拼成了一個矩形EFGH(如圖4),也推出sin75°= ![]() ,請你寫出小明或小麗推出sin75°=
,請你寫出小明或小麗推出sin75°= ![]() 的具體說理過程.
的具體說理過程.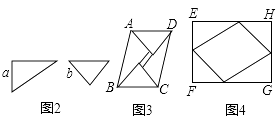
(3)【應(yīng)用】
在四邊形ABCD中,AD∥BC,∠D=75°,BC=6,CD=5,AD=10(如圖5)
①點(diǎn)E在AD上,設(shè)t=BE+CE,求t2的最小值;
②點(diǎn)F在AB上,將△BCF沿CF翻折,點(diǎn)B落在AD上的點(diǎn)G處,點(diǎn)G是AD的中點(diǎn)嗎?說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如果兩個角的差的絕對值等于![]() ,就稱這兩個角互為反余角,其中一個角叫做另一個角的反余角,例如,
,就稱這兩個角互為反余角,其中一個角叫做另一個角的反余角,例如,![]() ,
,![]() ,
,![]() ,則
,則![]() 和
和![]() 互為反余角,其中
互為反余角,其中![]() 是
是![]() 的反余角,
的反余角,![]() 也是
也是![]() 的反余角.
的反余角.
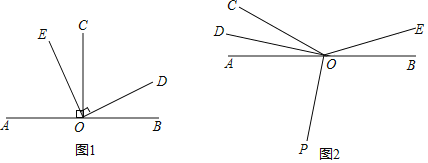
![]() 如圖
如圖![]() 為直線AB上一點(diǎn),
為直線AB上一點(diǎn),![]() 于點(diǎn)O,
于點(diǎn)O,![]() 于點(diǎn)O,則
于點(diǎn)O,則![]() 的反余角是______,
的反余角是______,![]() 的反余角是______;
的反余角是______;
![]() 若一個角的反余角等于它的補(bǔ)角的
若一個角的反余角等于它的補(bǔ)角的![]() ,求這個角.
,求這個角.
![]() 如圖2,O為直線AB上一點(diǎn),
如圖2,O為直線AB上一點(diǎn),![]() ,將
,將![]() 繞著點(diǎn)O以每秒
繞著點(diǎn)O以每秒![]() 角的速度逆時針旋轉(zhuǎn)得
角的速度逆時針旋轉(zhuǎn)得![]() ,同時射線OP從射線OA的位置出發(fā)繞點(diǎn)O以每秒
,同時射線OP從射線OA的位置出發(fā)繞點(diǎn)O以每秒![]() 角的速度逆時針旋轉(zhuǎn),當(dāng)射線OP與射線OB重合時旋轉(zhuǎn)同時停止,若設(shè)旋轉(zhuǎn)時間為t秒,求當(dāng)t為何值時,
角的速度逆時針旋轉(zhuǎn),當(dāng)射線OP與射線OB重合時旋轉(zhuǎn)同時停止,若設(shè)旋轉(zhuǎn)時間為t秒,求當(dāng)t為何值時,![]() 與
與![]() 互為反余角
互為反余角![]() 圖中所指的角均為小于平角的角
圖中所指的角均為小于平角的角![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
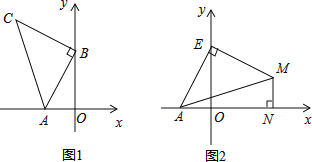
【題目】如圖1,![]() ,
,![]() ,以B點(diǎn)為直角頂點(diǎn)在第二象限作等腰直角
,以B點(diǎn)為直角頂點(diǎn)在第二象限作等腰直角![]() .
.
![]() 求C點(diǎn)的坐標(biāo);
求C點(diǎn)的坐標(biāo);
![]() 在坐標(biāo)平面內(nèi)是否存在一點(diǎn)P,使
在坐標(biāo)平面內(nèi)是否存在一點(diǎn)P,使![]() 與
與![]() 全等?若存在,直接寫出P點(diǎn)坐標(biāo),若不存在,請說明理由;
全等?若存在,直接寫出P點(diǎn)坐標(biāo),若不存在,請說明理由;
![]() 如圖2,點(diǎn)E為y軸正半軸上一動點(diǎn),以E為直角頂點(diǎn)作等腰直角
如圖2,點(diǎn)E為y軸正半軸上一動點(diǎn),以E為直角頂點(diǎn)作等腰直角![]() ,過M作
,過M作![]() 軸于N,直接寫出
軸于N,直接寫出![]() 的值為 .
的值為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
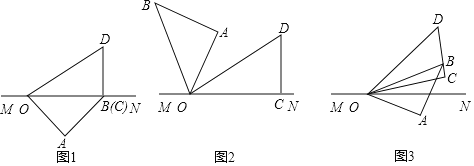
【題目】將一副三角板如圖1擺放在直線MN上,在三角板OAB和三角板OCD中,![]() ,
,![]() ,
,![]() .
.
![]() 保持三角板OCD不動,將三角板OAB繞點(diǎn)O以每秒
保持三角板OCD不動,將三角板OAB繞點(diǎn)O以每秒![]() 的速度逆時針旋轉(zhuǎn),旋轉(zhuǎn)時間為t秒.
的速度逆時針旋轉(zhuǎn),旋轉(zhuǎn)時間為t秒.
![]() 當(dāng)
當(dāng)![]() ______秒時,OB平分
______秒時,OB平分![]() 此時
此時![]() ______
______![]() ;
;
![]() 當(dāng)三角板OAB旋轉(zhuǎn)至圖2的位置,此時
當(dāng)三角板OAB旋轉(zhuǎn)至圖2的位置,此時![]() 與
與![]() 有怎樣的數(shù)量關(guān)系?請說明理由;
有怎樣的數(shù)量關(guān)系?請說明理由;
![]() 如圖3,若在三角板OAB開始旋轉(zhuǎn)的同時,另一個三角板OCD也繞點(diǎn)O以每秒
如圖3,若在三角板OAB開始旋轉(zhuǎn)的同時,另一個三角板OCD也繞點(diǎn)O以每秒![]() 的速度逆時針旋轉(zhuǎn),當(dāng)OB旋轉(zhuǎn)至射線OM上時同時停止.
的速度逆時針旋轉(zhuǎn),當(dāng)OB旋轉(zhuǎn)至射線OM上時同時停止.
![]() 當(dāng)t為何值時,OB平分
當(dāng)t為何值時,OB平分![]() ?
?
![]() 直接寫出在旋轉(zhuǎn)過程中,
直接寫出在旋轉(zhuǎn)過程中,![]() 與
與![]() 之間的數(shù)量關(guān)系.
之間的數(shù)量關(guān)系.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
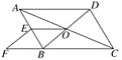
【題目】如圖,在ABCD中,對角線AC,BD交于點(diǎn)O,E為AB中點(diǎn),點(diǎn)F在CB的延長線上,且EF∥BD.
(1)求證:四邊形OBFE是平行四邊形;
(2)當(dāng)線段AD和BD之間滿足什么條件時,四邊形OBFE是矩形?并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】兩個大小不同的等腰直角三角形三角板如圖![]() 所示放置,圖
所示放置,圖![]() 是由它抽象出的幾何圖形,B,C,E在同一條直線上,聯(lián)結(jié)DC,
是由它抽象出的幾何圖形,B,C,E在同一條直線上,聯(lián)結(jié)DC,
![]() 請找出圖
請找出圖![]() 中的全等三角形,并給予說明
中的全等三角形,并給予說明![]() 說明:結(jié)論中不得含有未標(biāo)識的字母
說明:結(jié)論中不得含有未標(biāo)識的字母![]() ;
;
![]() 試說明:
試說明:![]() .
.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點(diǎn)D是邊AC上一點(diǎn),BC=BD=AD,則∠A的大小是( ).

A. 36° B. 54° C. 72° D. 30°
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com