
【題目】如圖,點![]() 在⊙
在⊙![]() 的直徑
的直徑![]() 的延長線上,點
的延長線上,點![]() 在⊙
在⊙![]() 上,
上, ![]() ,
, ![]() .
.
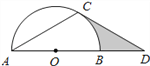
(1)求證: ![]() 是⊙
是⊙![]() 的切線;
的切線;
(2)若⊙![]() 的半徑為
的半徑為![]() ,求圖中陰影部分的面積.
,求圖中陰影部分的面積.
【答案】(1)證明見解析(2)![]()
【解析】試題分析:(1)連接OC.只需證明∠OCD=90°.根據等腰三角形的性質即可證明;
(2)先根據直角三角形中30°的銳角所對的直角邊是斜邊的一半求出OD,然后根據勾股定理求出CD,則陰影部分的面積即為直角三角形OCD的面積減去扇形COB的面積.
(1)證明:連接OC.

∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=∠ACD-∠2=90°,
即OC⊥CD,
∴CD是⊙O的切線;
(2)解:∠1=∠2+∠A=60°.
∴S扇形BOC=![]() =
=![]() .
.
在Rt△OCD中,∠D=30°,
∴OD=2OC=4,
∴CD=![]() =
=![]() .
.
∴SRt△OCD=![]() OC×CD=
OC×CD=![]() ×2×
×2×![]() =
=![]() .
.
∴圖中陰影部分的面積為: ![]() -
-![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖是人字型金屬屋架的示意圖,該屋架由BC、AC、BA、AD四段金屬材料焊接而成,其中A、B、C、D四點均為焊接點,且AB=AC,D為BC的中點,假設焊接所需的四段金屬材料已截好,并已標出BC段的中點D,那么,如果焊接工身邊只有可檢驗直角的角尺,而又為了準確快速地焊接,他應該首先選取的兩段金屬材料及焊接點是( )
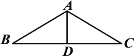
A.AB和AD,點AB.AB和AC,點B
C.AC和BC, 點CD.AD和BC,點D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在矩形![]() 中,點
中,點![]() 為
為![]() 邊中點,點
邊中點,點![]() 為
為![]() 邊中點;點
邊中點;點![]() ,
, ![]() 為
為![]() 邊三等分點,
邊三等分點, ![]() ,
, ![]() 為
為![]() 邊三等分點.小瑞分別用不同的方式連接矩形對邊上的點,如圖2,圖3所示.那么,圖2中四邊形
邊三等分點.小瑞分別用不同的方式連接矩形對邊上的點,如圖2,圖3所示.那么,圖2中四邊形![]() 的面積與圖3中四邊形
的面積與圖3中四邊形![]() 的面積相等嗎?
的面積相等嗎?
(1)小瑞的探究過程如下
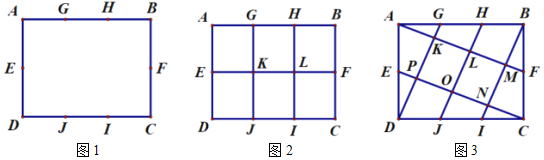
在圖2中,小瑞發現, ![]() ;
;
在圖3中,小瑞對四邊形![]() 面積的探究如下. 請你將小瑞的思路填寫完整:
面積的探究如下. 請你將小瑞的思路填寫完整:
設![]() ,
, ![]()
∵![]()
∴![]() ,且相似比為
,且相似比為![]() ,得到
,得到![]()
∵![]()
∴![]() ,且相似比為
,且相似比為![]() ,得到
,得到![]()
又∵![]() ,
, ![]()
∴![]()
∴![]() ,
, ![]() ,
, ![]()
∴![]() ,則
,則![]() (填寫“
(填寫“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)
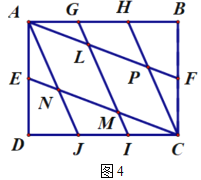
(2)小瑞又按照圖4的方式連接矩形![]() 對邊上的點.則
對邊上的點.則![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 垂直平分線段
垂直平分線段![]() (
(![]() ),點
),點![]() 是線段
是線段![]() 延長線上的一點,且
延長線上的一點,且![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,交
,交![]() 的延長線與點
的延長線與點![]() .
.

(1)若![]() ,則
,則![]() ______(用
______(用![]() 的代數式表示);
的代數式表示);
(2)線段![]() 與線段
與線段![]() 相等嗎?為什么?
相等嗎?為什么?
(3)若![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下表:
序號 | 1 | 2 | 3 | … |
圖形 |
|
|
| … |
我們把某格中字母和所得到的多項式稱為“特征多項式”,例如第1格的“特征多項式”為![]() .
.
回答下列問題:
(1)第3格的“特征多項式”為____________,
第4格的“特征多項式”為____________,
第![]() 格的“特征多項式”為____________;
格的“特征多項式”為____________;
(2)若第1格的“特征多項式”的值為10,第2格的“特征多項式”的值為19,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將正整數1至2019按照一定規律排成下表:

記aij表示第i行第j個數,如a14=4表示第1行第4個數是4.
(1)直接寫出a42= ,a53= ;
(2)①如果aij=2019,那么i= ,j= ;②用i,j表示aij= ;
(3)將表格中的5個陰影格子看成一個整體并平移,所覆蓋的5個數之和能否等于2027.若能,求出這5個數中的最小數,若不能說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上A點表示數a,B點表示數b,AB表示A點和B點之間的距離,C是AB的中點,且a、b滿足|a+3|+(b+3a)2=0.
(1)求點C表示的數;
(2)點P從A點以3個單位每秒向右運動,點Q同時從B點以2個單位每秒向左運動,若AP+BQ=2PQ,求時間t;
(3)若點P從A向右運動,點M為AP中點,在P點到達點B之前:①![]() 的值不變;②2BM﹣BP的值不變,其中只有一個正確,請你找出正確的結論并求出其值.
的值不變;②2BM﹣BP的值不變,其中只有一個正確,請你找出正確的結論并求出其值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 中的點P和圖形G,給出如下的定義:若在圖形G上存在一點Q ,使得P、Q之間的距離等于1,則稱P為圖形G的關聯點.
中的點P和圖形G,給出如下的定義:若在圖形G上存在一點Q ,使得P、Q之間的距離等于1,則稱P為圖形G的關聯點.
(1)當⊙O的半徑為1時:
①點![]() ,
, ![]() ,
, ![]() 中,⊙O的關聯點有_____________________.
中,⊙O的關聯點有_____________________.
②直線經過(0,1)點,且與![]() 軸垂直,點P在直線上.若P是⊙O的關聯點,求點P的橫坐標
軸垂直,點P在直線上.若P是⊙O的關聯點,求點P的橫坐標![]() 的取值范圍.
的取值范圍.
(2)已知正方形ABCD的邊長為4,中心為原點,正方形各邊都與坐標軸垂直.若正方形各邊上的點都是某個圓的關聯點,求圓的半徑![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com