Question

【題目】如圖，一次函數 分別交y軸、x軸于A、B兩點，拋物線y=﹣x2+bx+c過A、B兩點．

（1）求這個拋物線的解析式；
（2）作垂直x軸的直線x=t，在第一象限交直線AB于M，交這個拋物線于N．求當t取何值時，MN有最大值？最大值是多少？
（3）在（2）的情況下，以A、M、N、D為頂點作平行四邊形，求第四個頂點D的坐標．

Answer 1

【答案】
（1）解：∵ 分別交y軸、x軸于A.、B兩點，
∴A、B點的坐標為：A(0,2)，B(4,0)，
將x=0，y=2代入y=x+bx+c得c=2，
將x=4，y=0，c=2代入y=x+bx+c得0=16+4b+2，解得b= ，
∴拋物線解析式為：
（2）解：如圖1，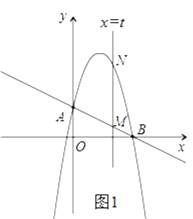

由題意可知，直線MN即是直線 ，
∵點M在直線 上，點N在拋物線 上，
∴點M、N的坐標分別為 、 ，
∵在第一象限中，點N在點M的上方，
∴MN= ，
∴當 時，MN最長=4；
（3）解：由（2）可知，A(0，2)，M(2，1)，N(2，5).
以A. M、N、D為頂點作平行四邊形，D點的可能位置有三種情形，如圖2所示：

(i)當D在y軸上時，設D的坐標為(0，a)
由AD=MN，得|a2|=4，解得a1=6，a2=2，
從而D1為(0，6)或D2(0，2)，
(ii)當D不在y軸上時，由圖可知D3為D1N與D2M的交點，
由D1、D2、M、N的坐標可求得直線D1N的解析式為：y= x+6，直線D2M的解析式為：y= x2，
由 解得 ，
∴D3的坐標為：(4，4)，
綜上所述，所求的D點坐標為(0，6)，(0，2)或(4，4)
【解析】（1）通過直線解析式求出A、B 兩點坐標，代入拋物線解析式，運用待定系數法求出拋物線解析式;（2）最值問題可構建以M的橫坐標t為自變量的函數，用t的代數式表示豎直線段MN ,應用配方法求出最值；（3）以A. M、N、D為頂點作平行四邊形，D點的位置需分類討論，分別以AM、AN、MN為對角線，另兩線段為邊，作出平行四邊形，共三種情況，利用直線的交點構建方程組，求出坐標.