
【題目】甲、乙兩人先后從公園大門出發,沿綠道向碼頭步行,乙先到碼頭并在原地等甲到達.圖1是他們行走的路程y(m)與甲出發的時間x(min)之間的函數圖象.
(1)求線段AC對應的函數表達式;
(2)寫出點B的坐標和它的實際意義;
(3)設d(m)表示甲、乙之間的距離,在圖2中畫出d與x之間的函數圖象(標注必要數據).

【答案】(1)y=100x﹣600;(2)點B的坐標為(15,900),它的實際意義是當甲出發15分鐘后被乙追上,此時他們距出發點900米;(3)d=60x;d=﹣40x+600;d=40x﹣600;d=1500﹣60x.
【解析】
(1)根據圖1中的數據可以得出線段AC對應的函數表達式;
(2)設直線OD的解析式為y=mx,將D(25,1500)代入,求出m的值,再聯立一次函數y=100x﹣600,即可求出B的坐標;
(3)分情況討論x的求值范圍并求出相對應的函數關系式.
解:(1)設線段AC對應的函數表達式為y=kx+b(k≠0).
將A(6,0)、C(21,1500)代入,
得![]() ,解得
,解得![]() ,
,
所以線段AC對應的函數表達式為y=100x﹣600;
(2)設直線OD的解析式為y=mx,
將D(25,1500)代入,
得25m=1500,解得m=60,
∴直線OD的解析式為y=60x.
由![]() ,解得
,解得![]() ,
,
∴點B的坐標為(15,900),它的實際意義是當甲出發15分鐘后被乙追上,此時他們距出發點900米;
(3)①當0≤x≤6時,d=60x;
②當6<x≤15時,d=60x﹣(100x﹣600)=﹣40x+600;
③當15<x≤21時,d=100x﹣600﹣60x=40x﹣600;
④當21<x≤25時,d=1500﹣60x.
d與x之間的函數圖象如圖所示:


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某班13位同學參加每周一次的衛生大掃除,按學校的衛生要求需要完成總面積為60m2的三個項目的任務,三個項目的面積比例和每人每分鐘完成各項目的工作量如圖所示: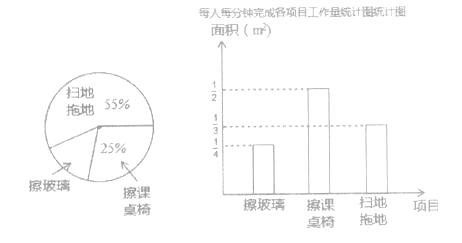
(1)從統計圖中可知:擦玻璃的面積占總面積的百分比為 , 每人每分鐘擦課桌椅
m2;
(2)掃地拖地的面積是m2;
(3)他們一起完成掃地和拖地任務后,把這13人分成兩組,一組去擦玻璃,一組去擦課桌椅,如果你是衛生委員,該如何分配這兩組的人數,才能最快地完成任務?(要有詳細的解答過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了讓同學們了解自己的體育水平,初二1班的體育劉老師對全班45名學生進行了一次體育模擬測試(得分均為整數),成績滿分為10分,1班的體育委員根據這次測試成績,制作了統計圖和分析表如下:
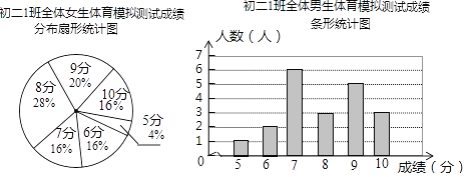
初二1班體育模擬測試成績分析表
平均分 | 方差 | 中位數 | 眾數 | |
男生 | 2 | 8 | 7 | |
女生 | 7.92 | 1.99 | 8 |
根據以上信息,解答下列問題:
(1)這個班共有男生________人,共有女生________人;
(2)補全初二1班體育模擬測試成績分析表.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖描述了某汽車在行駛過程中速度與時間的關系,下列說法中正確的是________.(填序號)

①第3分鐘時,汽車的速度是40千米/時;
②第12分鐘時,汽車的速度是0千米/時;
③從第3分鐘到第6分鐘,汽車行駛了120千米;
④從第9分鐘到第12分鐘,汽車的速度從60千米/時減小到0千米/時.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市為了節約用水,采用分段收費標準.若某戶居民每月應交水費y(元)與用水量x(噸)之間關系的圖象如圖,根據圖象回答:
(1)該市自來水收費時,若使用不足5噸,則每噸收費多少元?超過5噸部分每噸收費多少元?
(2)若某戶居民每月用水3.5噸,應交水費多少元?若某月交水費17元,該戶居民用水多少噸?
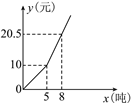
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是O的直徑,AE交O于點E,且與O的切線CD互相垂直,垂足為D. 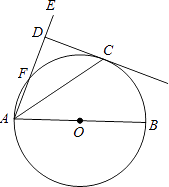
(1)求證:∠EAC=∠CAB;
(2)若CD=4,AD=8:①求O的半徑;②求tan∠BAE的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點B、C、E在同一條直線上,△ABC與△CDE都是等邊三角形,則下列結論不一定成立的是( ) 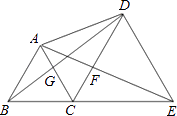
A.△ACE≌△BCD
B.△BGC≌△AFC
C.△DCG≌△ECF
D.△ADB≌△CEA
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,CD是⊙O的切線,切點為C.延長AB交CD于點E.連接AC,作∠DAC=∠ACD,作AF⊥ED于點F,交⊙O于點G. 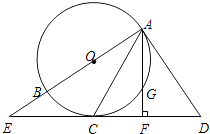
(1)求證:AD是⊙O的切線;
(2)如果⊙O的半徑是6cm,EC=8cm,求GF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,以BC為邊作等邊△BDC,連接AD.
(1)如圖1,直接寫出∠ADB的度數 ;
(2)如圖2,作∠ABM=60°在BM上截取BE,使BE=BA,連接CE,判斷CE與AD的數量關系,請補全圖形,并加以證明;
(3)在(2)的條件下,連接DE,AE.若∠DEC=60°,DE=2,求AE的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com