
【題目】如圖,AB是O的直徑,AE交O于點E,且與O的切線CD互相垂直,垂足為D. 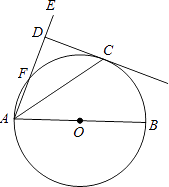
(1)求證:∠EAC=∠CAB;
(2)若CD=4,AD=8:①求O的半徑;②求tan∠BAE的值.
【答案】
(1)證明:連接OC.
∵CD是⊙O的切線,
∴CD⊥OC,
又∵CD⊥AE,
∴OC∥AE,
∴∠1=∠3,
∵OC=OA,
∴∠2=∠3,
∴∠1=∠2,
即∠EAC=∠CAB;
(2)解:

①連接BC.
∵AB是⊙O的直徑,CD⊥AE于點D,
∴∠ACB=∠ADC=90°,
∵∠1=∠2,
∴△ACD∽△ABC,
∴ ![]() ,
,
∵AC2=AD2+CD2=42+82=80,
∴AB= ![]() =10,
=10,
∴⊙O的半徑為10÷2=5.
②連接CF與BF.
∵四邊形ABCF是⊙O的內接四邊形,
∴∠ABC+∠AFC=180°,
∵∠DFC+∠AFC=180°,
∴∠DFC=∠ABC,
∵∠2+∠ABC=90°,∠DFC+∠DCF=90°,
∴∠2=∠DCF,
∵∠1=∠2,
∴∠1=∠DCF,
∵∠CDF=∠CDF,
∴△DCF∽△DAC,
∴ ![]() ,
,
∴DF= ![]() =2,
=2,
∴AF=AD﹣DF=8﹣2=6,
∵AB是⊙O的直徑,
∴∠BFA=90°,
∴BF= ![]() =8,
=8,
∴tan∠BAD= ![]() .
.
【解析】(1)首先連接OC,由CD是⊙O的切線,CD⊥OC,又由CD⊥AE,即可判定OC∥AE,根據平行線的性質與等腰三角形的性質,即可證得∠EAC=∠CAB;(2)①連接BC,易證得△ACD∽△ABC,根據相似三角形的對應邊成比例,即可求得AB的長,繼而可得⊙O的半徑長;②連接CF與BF.由四邊形ABCF是⊙O的內接四邊形,易證得△DCF∽△DAC,然后根據相似三角形的對應邊成比例,求得AF的長,又由AB是⊙O的直徑,即可得∠BFA是直角,利用勾股定理求得BF的長,即可求得tan∠BAE的值.
【考點精析】認真審題,首先需要了解勾股定理的概念(直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2),還要掌握圓周角定理(頂點在圓心上的角叫做圓心角;頂點在圓周上,且它的兩邊分別與圓有另一個交點的角叫做圓周角;一條弧所對的圓周角等于它所對的圓心角的一半)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】老王的魚塘里年初養了某種魚2000條,到年底捕撈出售,為了估計魚的總產量,從魚塘里捕撈了三次,得到如下表的數據:
魚的條數 | 平均每條魚的質量 | |
第一次捕撈 | 10 | 1.7千克 |
第二次捕撈 | 25 | 1.8千克 |
第三次捕撈 | 15 | 2.0千克 |
若老王放養這種魚的成活率是95%,則:
(1)魚塘里這種魚平均每條重約多少千克?
(2)魚塘里這種魚的總產量是多少千克?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過點A(2,0)的兩條直線![]() ,
,![]() 分別交
分別交![]() 軸于B,C,其中點B在原點上方,點C在原點下方,已知AB=
軸于B,C,其中點B在原點上方,點C在原點下方,已知AB=![]() .
.

(1)求點B的坐標;
(2)若△ABC的面積為4,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明同學騎自行車去郊外春游,騎行1小時后,自行車出現故障,維修好后繼續騎行,下圖表示他離家的距離y(千米)與所用的時間x(時)之間關系的圖象.
(1)根據圖象回答:小明到達離家最遠的地方用了多長時間?此時離家多遠?
(2)求小明出發2.5小時后離家多遠;
(3)求小明出發多長時間離家12千米.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人先后從公園大門出發,沿綠道向碼頭步行,乙先到碼頭并在原地等甲到達.圖1是他們行走的路程y(m)與甲出發的時間x(min)之間的函數圖象.
(1)求線段AC對應的函數表達式;
(2)寫出點B的坐標和它的實際意義;
(3)設d(m)表示甲、乙之間的距離,在圖2中畫出d與x之間的函數圖象(標注必要數據).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解市民“獲取新聞的最主要途徑”某市記者開展了一次抽樣調查,根據調查結果繪制了如下尚不完整的統計圖.
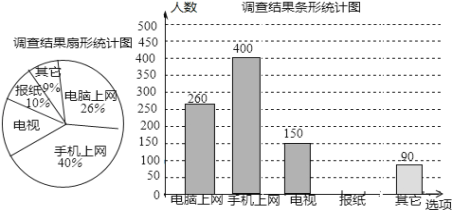
根據以上信息解答下列問題:
(1)這次接受調查的市民總人數是 ;請補全條形統計圖;
(2)扇形統計圖中,“電視”所對應的圓心角的度數是 ;
(3)若該市約有90萬人,請你估計其中將“電腦和手機上網”作為“獲取新聞的最主要途徑”的總人數。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知拋物線y=ax2+bx﹣8與x軸交于兩點A,B,與y軸交于點C,直線l經過坐標原點O,與拋物線的一個交點為點D,與拋物線的對稱軸交于點E,連接CE,已知點A,D的坐標分別為(﹣2,0),(6,﹣8).
(1)求拋物線的函數表達式;
(2)求點E的坐標;
(3)試探究在x軸下方的拋物線上是否存在點F,使得△FOB和△EOB的面積相等,若存在,請求出點F的坐標,若不存在,請說明理由;
(4)若點P是y軸負半軸上的一個動點,設其坐標為(0,m),直線PB與直線l交于點Q,請直接寫出:當m為何值時,△OPQ是等腰三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com