
【題目】如圖,已知拋物線y=ax2+bx+c(a>0,c<0)交x軸于點A,B,交y軸于點C,設過點A,B,C三點的圓與y軸的另一個交點為D.
(1)如圖1,已知點A,B,C的坐標分別為(﹣2,0),(8,0),(0,﹣4);
①求此拋物線的表達式與點D的坐標;
②若點M為拋物線上的一動點,且位于第四象限,求△BDM面積的最大值;
(2)如圖2,若a=1,求證:無論b,c取何值,點D均為定點,求出該定點坐標.
【答案】
(1)
解:∵拋物線y=ax2+bx+c過點A(﹣2,0),B(8,0),C(0,﹣4),
∴ 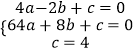 ,解得
,解得 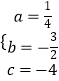 ,
,
∴拋物線的解析式為:y= ![]() x2﹣
x2﹣ ![]() x﹣4;
x﹣4;
∵OA=2,OB=8,OC=4,∴AB=10.
如答圖1,連接AC、BC.
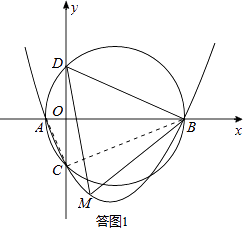
由勾股定理得:AC= ![]() ,BC=
,BC= ![]() .
.
∵AC2+BC2=AB2=100,
∴∠ACB=90°,
∴AB為圓的直徑.
由垂徑定理可知,點C、D關于直徑AB對稱,
∴D(0,4).
解法一:
設直線BD的解析式為y=kx+b,∵B(8,0),D(0,4),
∴ ![]() ,解得
,解得 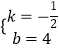 ,
,
∴直線BD解析式為:y=﹣ ![]() x+4.
x+4.
設M(x, ![]() x2﹣
x2﹣ ![]() x﹣4),
x﹣4),
如答圖2﹣1,過點M作ME∥y軸,交BD于點E,則E(x,﹣ ![]() x+4).
x+4).
∴ME=(﹣ ![]() x+4)﹣(
x+4)﹣( ![]() x2﹣
x2﹣ ![]() x﹣4)=﹣
x﹣4)=﹣ ![]() x2+x+8.
x2+x+8.
∴S△BDM=S△MED+S△MEB= ![]() ME(xE﹣xD)+
ME(xE﹣xD)+ ![]() ME(xB﹣xE)=
ME(xB﹣xE)= ![]() ME(xB﹣xD)=4ME,
ME(xB﹣xD)=4ME,
∴S△BDM=4(﹣ ![]() x2+x+8)=﹣x2+4x+32=﹣(x﹣2)2+36.
x2+x+8)=﹣x2+4x+32=﹣(x﹣2)2+36.
∴當x=2時,△BDM的面積有最大值為36;
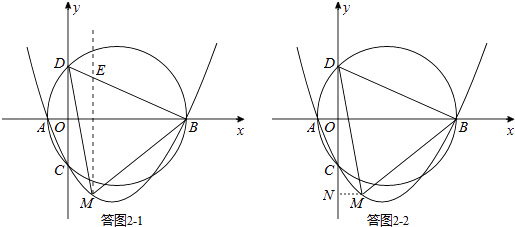
解法二:
如答圖2﹣2,過M作MN⊥y軸于點N.
設M(m, ![]() m2﹣
m2﹣ ![]() m﹣4),
m﹣4),
∵S△OBD= ![]() OBOD=
OBOD= ![]() =16,
=16,
S梯形OBMN= ![]() (MN+OB)ON
(MN+OB)ON
= ![]() (m+8)[﹣(
(m+8)[﹣( ![]() m2﹣
m2﹣ ![]() m﹣4)]
m﹣4)]
=﹣ ![]() m(
m( ![]() m2﹣
m2﹣ ![]() m﹣4)﹣4(
m﹣4)﹣4( ![]() m2﹣
m2﹣ ![]() m﹣4),
m﹣4),
S△MND= ![]() MNDN
MNDN
= ![]() m[4﹣(
m[4﹣( ![]() m2﹣
m2﹣ ![]() m﹣4)]
m﹣4)]
=2m﹣ ![]() m(
m( ![]() m2﹣
m2﹣ ![]() m﹣4),
m﹣4),
∴S△BDM=S△OBD+S梯形OBMN﹣S△MND
=16﹣ ![]() m(
m( ![]() m2﹣
m2﹣ ![]() m﹣4)﹣4(
m﹣4)﹣4( ![]() m2﹣
m2﹣ ![]()
![]() m(
m( ![]() m2﹣
m2﹣ ![]() m﹣4)
m﹣4)
=16﹣4( ![]() m2﹣
m2﹣ ![]() m﹣4)﹣2m
m﹣4)﹣2m
=﹣m2+4m+32
=﹣(m﹣2)2+36;
∴當m=2時,△BDM的面積有最大值為36.
(2)
解:如答圖3,連接AD、BC.
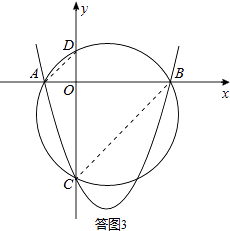
由圓周角定理得:∠ADO=∠CBO,∠DAO=∠BCO,
∴△AOD∽△COB,
∴ ![]() =
= ![]() ,
,
設A(x1,0),B(x2,0),
∵已知拋物線y=x2+bx+c(c<0),
∵OC=﹣c,x1x2=c,
∴ ![]() =
= ![]() ,
,
∴OD= ![]() =1,
=1,
∴無論b,c取何值,點D均為定點,該定點坐標D(0,1).
【解析】(1)①利用待定系數法求拋物線的解析式;利用勾股定理的逆定理證明∠ACB=90°,由圓周角定理得AB為圓的直徑,再由垂徑定理知點C、D關于AB對稱,由此得出點D的坐標;②求出△BDM面積的表達式,再利用二次函數的性質求出最值.解答中提供了兩種解法,請分析研究;(2)根據拋物線與x軸的交點坐標、根與系數的關系、相似三角形求解.
【考點精析】本題主要考查了二次函數的圖象和二次函數的性質的相關知識點,需要掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】鹽城電視塔是我市標志性建筑之一.如圖,在一次數學課外實踐活動中,老師要求測電視塔的高度AB.小明在D處用高1.5m的測角儀CD,測得電視塔頂端A的仰角為30°,然后向電視塔前進224m到達E處,又測得電視塔頂端A的仰角為60°.求電視塔的高度AB.( ![]() 取1.73,結果精確到0.1m)
取1.73,結果精確到0.1m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的弦,OP⊥OA交AB于點P,過點B的直線交OP的延長線于點C,且CP=CB. 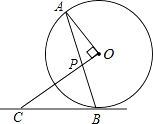
(1)求證:BC是⊙O的切線;
(2)若⊙O的半徑為 ![]() ,OP=1,求BC的長.
,OP=1,求BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解“數學思想作為對學習數學幫助有多大?”一研究員隨機抽取了一定數量的高校大一學生進行了問卷調查,并將調查得到的數據用下面的扇形圖和下表來表示(圖、表都沒制作完成). 
選項 | 幫助很大 | 幫助較大 | 幫助不大 | 幾乎沒有幫助 |
人數 | a | 543 | 269 | b |
根據圖、表提供的信息.
(1)請問:這次共有多少名學生參與了問卷調查?
(2)算出表中a、b的值. (注:計算中涉及到的“人數”均精確到1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為3cm,E為CD邊上一點,∠DAE=30°,M為AE的中點,過點M作直線分別與AD、BC相交于點P、Q.若PQ=AE,則AP等于cm. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知函數y= ![]() (x>0)的圖象經過點A、B,點A的坐標為(1,2),過點A作AC∥y軸,AC=1(點C位于點A的下方),過點C作CD∥x軸,與函數的圖象交于點D,過點B作BE⊥CD,垂足E在線段CD上,連接OC、OD.
(x>0)的圖象經過點A、B,點A的坐標為(1,2),過點A作AC∥y軸,AC=1(點C位于點A的下方),過點C作CD∥x軸,與函數的圖象交于點D,過點B作BE⊥CD,垂足E在線段CD上,連接OC、OD. 
(1)求△OCD的面積;
(2)當BE= ![]() AC時,求CE的長.
AC時,求CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+c過點(﹣2,2),(4,5),過定點F(0,2)的直線l:y=kx+2與拋物線交于A、B兩點,點B在點A的右側,過點B作x軸的垂線,垂足為C.
(1)求拋物線的解析式;
(2)當點B在拋物線上運動時,判斷線段BF與BC的數量關系(>、<、=),并證明你的判斷;
(3)P為y軸上一點,以B、C、F、P為頂點的四邊形是菱形,設點P(0,m),求自然數m的值;
(4)若k=1,在直線l下方的拋物線上是否存在點Q,使得△QBF的面積最大?若存在,求出點Q的坐標及△QBF的最大面積;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com