
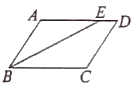
【題目】已知:在![]() 和
和![]() 中,
中,![]() ,
,![]() ,將
,將![]() 如圖擺放,使得
如圖擺放,使得![]() 的兩條邊分別經過點
的兩條邊分別經過點![]() 和點
和點![]() .
.

(1)當將![]() 如圖1擺放時,則
如圖1擺放時,則![]() _________度.
_________度.
(2)當將![]() 如圖2擺放時,請求出
如圖2擺放時,請求出![]() 的度數,并說明理由.
的度數,并說明理由.
(3)能否將![]() 擺放到某個位置時,使得
擺放到某個位置時,使得![]() 、
、![]() 同時平分
同時平分![]() 和
和![]() ?直接寫出結論_______(填“能”或“不能”)
?直接寫出結論_______(填“能”或“不能”)
【答案】(1)240;(2)![]() 理由見解析;(3)不能
理由見解析;(3)不能
【解析】
(1)要求∠ABD+∠ACD的度數,只要求出∠ABC+∠CBD+∠ACB+∠BCD,利用三角形內角和定理得出∠ABC+∠ACB=180°-∠A=180°-40°=140°;根據三角形內角和定理,∠CBD+∠BCD=∠E+∠F=100°,得出∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°;
(2)要求∠ABD+∠ACD的度數,只要求出∠ABC+∠ACB-(∠BCD+∠CBD)的度數.根據三角形內角和定理,∠CBD+∠BCD=∠E+∠F=100°;根據三角形內角和定理得,∠ABC+∠ACB=180°-∠A=140°,得出∠ABD+∠ACD=∠ABC+∠ACB-(∠BCD+∠CBD)=140°-100°=40°;
(3)不能.假設能將△DEF擺放到某個位置時,使得BD、CD同時平分∠ABC和∠ACB.則∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,與三角形內角和定理矛盾,所以不能.
(1)在△ABC中,∠A+∠ABC+∠ACB=180°,∠A=40°
∴∠ABC+∠ACB=180°∠A=180°40°=140°
在△BCD中,∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°∠D
在△DEF中,∠D+∠E+∠F=180°
∴∠E+∠F=180°∠D
∴∠CBD+∠BCD=∠E+∠F=100°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+100°=240°.
(2)∠ABD+∠ACD=40°;
理由如下:
∵∠E+∠F=100°
∴∠D=180°(∠E+∠F)=80°
∴∠ABD+∠ACD=180°∠A∠DBC∠DCB=180°40°(180°80°)=40°;
(3)不能.假設能將△DEF擺放到某個位置時,使得BD、CD同時平分∠ABC和∠ACB.則∠CBD+∠BCD=∠ABD+∠ACD=100°,那么∠ABC+∠ACB=200°,與三角形內角和定理矛盾,所以不能.


科目:初中數學 來源: 題型:
【題目】如圖,直線l1 :y=-3x+3與x軸交于點D,直線l2經過A(4,0)、B(3,![]() )兩點,直線l1 與直線l2交于點C.
)兩點,直線l1 與直線l2交于點C.
(1)求直線l2的解析式和點C的坐標;
(2)在 y軸上是否存在一點P,使得四邊形PDBC的周長最小?若存在,請求出點P的坐標,若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
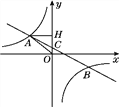
【題目】如圖,在平面直角坐標系中,一次函數y=ax+b(a≠0)的圖象與反比例函數y=![]() (k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=
(k≠0)的圖象交于第二、四象限內的A、B兩點,與y軸交于C點,過點A作AH⊥y軸,垂足為H,OH=3,tan∠AOH=![]() ,點B的坐標為(m,-2).
,點B的坐標為(m,-2).
(1)求△AHO的周長;
(2)求該反比例函數和一次函數的解析式.
【答案】(1)△AHO的周長為12;(2) 反比例函數的解析式為y=![]() ,一次函數的解析式為y=-
,一次函數的解析式為y=-![]() x+1.
x+1.
【解析】試題分析: (1)根據正切函數,可得AH的長,根據勾股定理,可得AO的長,根據三角形的周長,可得答案;
(2)根據待定系數法,可得函數解析式.
試題解析:(1)由OH=3,tan∠AOH=![]() ,得
,得
AH=4.即A(-4,3).
由勾股定理,得
AO=![]() =5,
=5,
△AHO的周長=AO+AH+OH=3+4+5=12;
(2)將A點坐標代入y=![]() (k≠0),得
(k≠0),得
k=-4×3=-12,
反比例函數的解析式為y=![]() ;
;
當y=-2時,-2=![]() ,解得x=6,即B(6,-2).
,解得x=6,即B(6,-2).
將A、B點坐標代入y=ax+b,得
![]() ,
,
解得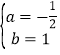 ,
,
一次函數的解析式為y=-![]() x+1.
x+1.
考點:反比例函數與一次函數的交點問題.
【題型】解答題
【結束】
21
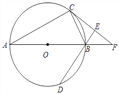
【題目】如圖,AB為⊙O的直徑,C、D為⊙O上不同于A、B的兩點,∠ABD=2∠BAC,過點C作CE⊥DB交DB的延長線于點E,直線AB與CE相交于點F.
(1)求證:CF為⊙O的切線;
(2)填空:當∠CAB的度數為________時,四邊形ACFD是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
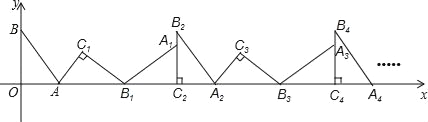
【題目】如圖,在平面直角坐標系中,將△ABO繞點A順時針旋轉到△AB1C1的位置,點B、O分別落在點B1、C1處,點B1在x軸上,再將△AB1C1繞點B1順時針旋轉到△A1B1C2的位置,點C2在x軸上,將△A1B1C2繞點C2順時針旋轉到△A2B2C2的位置,點A2在x軸上,依次進行下去….若點A(![]() ,0),B(0,2),則B2的坐標為_____;點B2016的坐標為_____.
,0),B(0,2),則B2的坐標為_____;點B2016的坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)操作發現:
如圖,在矩形ABCD中,E是BC的中點,將△ABE沿AE折疊后得到△AFE,點F在矩形ABCD內部,延長AF交CD于點G.猜想線段GF與GC有何數量關系?并證明你的結論.

(2)類比探究:
如圖,將(1)中的矩形ABCD改為平行四邊形,其它條件不變,(1)中的結論是否仍然成立?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在□ABCD中,O是對角線AC的中點,過O作AC的垂線與邊AD、BC分別交于E、F。
(1)求證:四邊形AFCE是菱形;
(2)若AF⊥BC,試猜想四邊形AFCE是什么特殊四邊形,并說明理由。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖已知BE平分∠ABC,E點在線段AD上,∠ABE=∠AEB,AD與BC平行嗎?為什么?
解:因為BE平分∠ABC(已知)
所以∠ABE=∠EBC ( )
因為∠ABE=∠AEB( )
所以∠ =∠ ( )
所以AD∥BC ( )
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,點
中,點![]() 的坐標為(0,4),線段
的坐標為(0,4),線段![]() 的位置如圖所示,其中點
的位置如圖所示,其中點![]() 的坐標為(
的坐標為(![]() ,
,![]() ),點
),點![]() 的坐標為(3,
的坐標為(3,![]() ).
).

(1)將線段![]() 平移得到線段
平移得到線段![]() ,其中點
,其中點![]() 的對應點為
的對應點為![]() ,點
,點![]() 的對應點為點
的對應點為點![]() .
.
①點![]() 平移到點
平移到點![]() 的過程可以是:先向 平移 個單位長度,再向 平移 個單位長度;
的過程可以是:先向 平移 個單位長度,再向 平移 個單位長度;
②點![]() 的坐標為 .
的坐標為 .
(2)在(1)的條件下,若點![]() 的坐標為(4,0),連接
的坐標為(4,0),連接![]() ,畫出圖形并求
,畫出圖形并求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com